Which is the correct factored form for 8x^3?
Answers
Answer:
HI! If this helps plz brainlist
Step-by-step explanation:
Rewrite 8 x 3 8 x 3 as (2x)3 ( 2 x ) 3 . Rewrite 27 as 33 . Since both terms are perfect cubes, factor using the difference of cubes formula, a3−b3=(a−b)(a2+ab+b2) a 3 - b 3 = ( a - b ) ( a 2 + a b + b 2 ) where a=2x a = 2 x and b=3 . Simplify.
Related Questions
7. suppose a binary digit (0 or 1) needs to be transmitted across a series of 4 channels. each time, the digit is transmitted correctly to the next channel with probability 0.9, and is transmitted incorrectly (meaning that 1 is transmitted as 0, and 0 is transmitted as 1) with probability 0.1. if the digit 0 is sent, what is the probability that the digit that is received (after having been transmitted across the 4 channels) is a 0?
Answers
The probability that the digit that is received (after having been transmitted across the 4 channels) is 0.3645
In communication systems, it is common to face the challenge of transmitting information accurately over a noisy channel. In this scenario, errors can occur during transmission, and it is essential to quantify the probability of receiving the correct information at the end of the channel.
In this problem, we are asked to calculate the probability that the digit received after transmitting a 0 across four channels is also a 0. We know that each channel can either transmit the digit correctly with probability 0.9 or incorrectly with probability 0.1. Therefore, we can use the concept of conditional probability to solve this problem.
Using Bayes' theorem, we can rewrite this as:
P(CCCC | 0 received) x P(0 received) / P(CCCC)
Here, P(CCCC | 0 received) represents the probability that all four channels transmitted the 0 correctly, given that a 0 was received. This probability can be calculated as:
P(CCCC | 0 received) = P(C) x P(C | C) x P(C | C | C) x P(C | C | C | C)
Substituting the given probabilities, we get:
P(CCCC | 0 received) = 0.9 * 0.9 * 0.9 * 0.9 = 0.6561
Similarly, we can calculate the probability of receiving a 0 in general as:
P(0 received) = P(CCCC | 0 received) x P(0) + P(IIII | 0 received) x P(1)
where P(IIII | 0 received) represents the probability that all four channels transmitted the digit incorrectly, given that a 0 was received. This probability can be calculated similarly as:
P(IIII | 0 received) = P(I) * P(I | I) x P(I | I | I) x P(I | I | I | I) = 0.1 x 0.1 x 0.1 x 0.1 = 0.0001
Substituting the given probabilities, we get:
P(0 received) = 0.6561 x 0.5 + 0.0001 x 0.5 = 0.3281
Finally, we can calculate the denominator P(CCCC) as:
P(CCCC) = P(CCCC | 0 received) x P(0) + P(CCCC | 1 received) x P(1)
where P(CCCC | 1 received) represents the probability that all four channels transmitted the digit correctly, given that a 1 was received. This probability can be calculated similarly as:
P(CCCC | 1 received) = P(I) x P(I | C) x P(I | C | C) x P(I | C | C | C) = 0.1 x 0.9 x 0.9 x 0.9 = 0.0729
Substituting the given probabilities, we get:
P(CCCC) = 0.6561 * 0.5 + 0.0729 * 0.5 = 0.3645
To know more about probability here.
https://brainly.com/question/11234923
#SPJ4
on a number line, √234 falls between which two numbers?
Answers
Root of 234 is roughly 15.3
Answer:
15 and 16
Step-by-step explanation:
sqrt(234) = 15.297
which falls between 15 and 16
Draw graph and answer please.

Answers
answer: (2,1) hope this helps

A firm that manufactures grape juice has a machine that automatically fills bottles. The mean of the process is assumed to be the machine's setting. The process variation (standard deviation) is 1.2 oz. (Assume that the process has a normal distribution.) B1. Customers get unhappy if the actual level is less than 36 oz but do not mind if it is greater than 36 oz. If you set the machine at 37 oz. what % of the time would the bottle contain less than 36 oz.?
B2. The bottle will actually hold 40 oz. If you set the machine to 38, what percent of the time will the bottles overflow?
B3. If 10 bottles from this process (setting at 38) are filled, what is the probability that at least one will have overflowed? (Use basic probability concepts.)
B4. If 15 bottles from this process (setting at 38) are filled, what is the probability that exactly 3 will have overflowed? (binomial)
B5. With the machine set at 38 oz., how big would the bottle have to be not to overflow 99.8% of the time?
Answers
B1. the bottle would contain less than 36 oz approximately 20.33% of the time when the machine is set at 37 oz.
B2. The bottles will overflow approximately 4.75% of the time when the machine is set at 38 oz.
B3. The probability that at least one bottle will overflow out of 10 bottles filled when the machine is set at 38 oz is approximately 99.9%.
B4. The probability that exactly 3 bottles will overflow out of 15 bottles filled when the machine is set at 38 oz is approximately 25.0%.
B5. The bottle would need to be approximately 40.796 oz or larger to avoid overflowing 99.8% of the time when the machine is set at 38 oz.
B1. To find the percentage of time the bottle contains less than 36 oz when the machine is set at 37 oz, we need to calculate the probability that a random bottle will have a volume less than 36 oz.
Using the normal distribution, we can calculate the z-score (standardized score) for 36 oz using the formula:
z = (x - μ) / σ
where x is the desired value (36 oz), μ is the mean of the process (37 oz), and σ is the standard deviation (1.2 oz).
z = (36 - 37) / 1.2
z ≈ -0.833
Using a standard normal distribution table or a statistical calculator, we can find the cumulative probability associated with this z-score.
P(X < 36) = P(Z < -0.833) ≈ 0.2033
Therefore, the bottle would contain less than 36 oz approximately 20.33% of the time when the machine is set at 37 oz.
B2. To find the percentage of time the bottles will overflow when the machine is set at 38 oz, we need to calculate the probability that a random bottle will have a volume greater than 40 oz.
Using the normal distribution, we can calculate the z-score for 40 oz using the formula mentioned earlier:
z = (x - μ) / σ
z = (40 - 38) / 1.2
z ≈ 1.67
Using a standard normal distribution table or a statistical calculator, we can find the cumulative probability associated with this z-score.
P(X > 40) = P(Z > 1.67) ≈ 0.0475
Therefore, the bottles will overflow approximately 4.75% of the time when the machine is set at 38 oz.
B3. To find the probability that at least one bottle will overflow out of 10 bottles filled when the machine is set at 38 oz, we can use the complement rule and subtract the probability that none of the bottles overflow.
The probability of no overflow in a single bottle is given by:
P(X ≤ 38) = P(Z ≤ (38 - 38) / 1.2) = P(Z ≤ 0) ≈ 0.5
Therefore, the probability of no overflow in 10 bottles is:
P(no overflow in 10 bottles) = (0.5)¹⁰ ≈ 0.00098
The probability that at least one bottle will overflow is the complement of no overflow:
P(at least one overflow in 10 bottles) = 1 - P(no overflow in 10 bottles) ≈ 1 - 0.00098 ≈ 0.999
Therefore, the probability that at least one bottle will overflow out of 10 bottles filled when the machine is set at 38 oz is approximately 99.9%.
B4. To find the probability that exactly 3 bottles will overflow out of 15 bottles filled when the machine is set at 38 oz, we can use the binomial distribution formula:
P(X = k) = (nCk) * \(p^k * (1 - p)^{(n - k)\)
where n is the number of trials (15), k is the desired number of successes (3), p is the probability of success (probability of overflow), and (nCk) is the number of combinations.
Using the probability of overflow calculated in B2:
p = 0.0475
The number of combinations for selecting 3 out of 15 bottles is given by:
15C3 = 15! / (3! * (15 - 3)!) = 455
Plugging the values into the binomial distribution formula:
P(X = 3) = 455 * (0.0475)³ * (1 - 0.0475)¹² ≈ 0.250
Therefore, the probability that exactly 3 bottles will overflow out of 15 bottles filled when the machine is set at 38 oz is approximately 25.0%.
B5. To determine the required size of the bottle to avoid overflowing 99.8% of the time when the machine is set at 38 oz, we need to find the z-score corresponding to a cumulative probability of 0.998.
Using a standard normal distribution table or a statistical calculator, we find the z-score for a cumulative probability of 0.998 to be approximately 2.33.
Using the formula mentioned earlier:
z = (x - μ) / σ
Substituting the known values:
2.33 = (x - 38) / 1.2
Solving for x:
x - 38 = 2.33 * 1.2
x - 38 ≈ 2.796
x ≈ 40.796
Therefore, the bottle would need to be approximately 40.796 oz or larger to avoid overflowing 99.8% of the time when the machine is set at 38 oz.
Learn more about probability here
https://brainly.com/question/31828911
#SPJ4
x^2+y^2=100 is it a function?
Answers
The equation x^2+y^2=100 is not a function
How to determine if it is a functionFrom the question, we have the following parameters that can be used in our computation:
x^2 + y^2 = 100
The above equation is a circle equation
As a general rule, we have
Circle equations are not functions and they do not represent a function on a graph
Hence, x^2+y^2=100 is not a function
Read more about function at
https://brainly.com/question/22340031
#SPJ1
A sandbox in the shape of a rectangular prism measures 11 feet by 7. 5 feet by 1. 5 feet. Find the maximum amount of sand the box can hold
Answers
The maximum amount of sand the rectangular prism sandbox can hold is 124.125 cubic feet.
To find the maximum amount of sand the rectangular prism sandbox can hold, we calculate its volume. The volume of a rectangular prism is given by the formula V = l × w × h, where l is the length, w is the width, and h is the height. In this case, the sandbox measures 11 feet by 7.5 feet by 1.5 feet.
Plugging in these values, we get V = 11 × 7.5 × 1.5 = 124.125 cubic feet. Therefore, the maximum amount of sand the sandbox can hold is 124.125 cubic feet. This represents the total space available inside the sandbox and indicates the maximum capacity for sand.
Learn more about a Prism here: brainly.com/question/12649592
#SPJ11
The partial derivative fx(-1, 0) of f(x, y) = xe³ + x² + 1 is equal to -1.
Select one:
True
False
Answers
The statement :-The partial derivative \(fx(-1, 0) of f(x, y) = xe³ + x² + 1\) is equal to -1” is False. In mathematics, the partial derivative is a derivative that includes various variables, and which holds the other variables constant.
The partial derivative is the slope of the tangent line to a point on a surface that lies on the plane of two variables. It is also known as the function’s derivative with respect to one of the two variables.
Let's solve the given problem,Given that;
\(f(x, y) = xe³ + x² + 1\)We need to find partial derivative fx (-1,0).
Let's find the partial derivative with respect to x,
\(f(x, y) = xe³ + x² + 1∂f/∂x = (3x² + 3e³x) + 2x\)
Now,Let’s evaluate the partial derivative
fx(-1, 0);\(f(x, y) = xe³ + x² + 1∂f/∂x = (3x² + 3e³x) + 2x= (3(-1)² + 3e³(-1)) + 2(-1)= (3+ 3e³) - 2= 3e³ + 1\)
∴ the partial derivative fx (-1,0) of f(x, y) is not equal to -1.
The given statement is False and the partial derivative fx(-1, 0) of \(f(x, y) = xe³ + x² + 1\)is not equal to -1.
To know more about partial derivative visit:-
https://brainly.com/question/32387059
#SPJ11
A fish tank in a nature center has a shape of a rectangular prism. The tank is 10 ft long, 8 1/4 ft wide and 6 ft tall. Show work pls

Answers
Answer:
Step-by-step explanation:
need more information
A bookshelf is 4-3/4 feet wide. how many 3-inch-wide books will fit on the shelf?
Answers
19 books can fit into a bookshelf that has a width of 19/4 feet
What is an equation?An equation is an expression that shows the relationship between two or more number and variables.
The bookshelf is 4 3/4 feet wide = 19/4 feet
1 ft = 12 in, hence:
19/4 feet = 19/4 feet * 12 in per feet = 57 inches
Number of books = 57 inches / 3 in = 19
19 books can fit into a bookshelf that has a width of 19/4 feet
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
Can someone help on this question from khanademy geometry. Finding the equation for the circle

Answers
The equation of the circle graphed in this problem is:
(x - 5)² + y² = 16.
What is the equation of a circle?The equation of a circle of center \((x_0, y_0)\) and radius r is given by:
\((x - x_0)^2 + (y - y_0)^2 = r^2\)
For the circle graphed, we have that:
The center is at point (5,0), hence \(x_0 = 5, y_0 = 0\).The radius is of 4 units.Hence the equation of the circle graphed is:
(x - 5)² + y² = 16.
More can be learned about the equation of a circle at https://brainly.com/question/24307696
#SPJ1
What is the value of
in the equation shown?
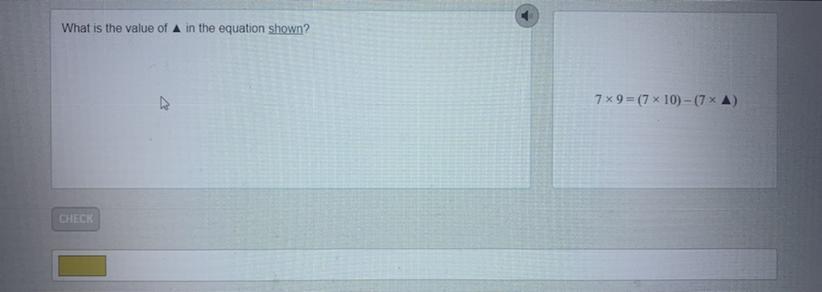
Answers

IV Find the citical points at which profit (pie) is maximized given the total revenue TR=4700−302 and Total CostTC =320/10,500 (2pts) 1. Compute Marginal Revenue and Marginal Cost 2. Equate MR=MC to find Q
∗
3. Verify that Q* is a relative maximum point 4. Compute the maximum profit level (pie) )
∗
by establishing (pie)* =9( (pie) (Q
∗
)
Answers
To find the critical points at which profit is maximized given the total revenue TR = 4700 - 302 and total cost TC = 320/10,500, we need to compute the marginal revenue and marginal cost, equate MR = MC to find the optimal quantity Q∗, verify if Q∗ is a relative maximum point, and compute the maximum profit level (π) by evaluating π∗ = 9(π(Q∗)).
Marginal Revenue (MR) is the derivative of the total revenue function with respect to quantity (Q). In this case, MR = dTR/dQ. By taking the derivative of TR = 4700 - 302 with respect to Q, we can find the expression for MR.
Marginal Cost (MC) is the derivative of the total cost function with respect to quantity (Q). In this case, MC = dTC/dQ. By taking the derivative of TC = 320/10,500 with respect to Q, we can find the expression for MC.
To find the optimal quantity Q∗, we equate MR and MC by setting MR = MC and solve for Q. This is because profit is maximized when MR equals MC.
Once we have found Q∗, we need to verify if it is a relative maximum point. This can be done by checking the second derivative of the profit function and determining if it is negative at Q∗. If the second derivative is negative, it confirms that Q∗ is a relative maximum point.
Finally, to compute the maximum profit level (π∗), we evaluate π(Q∗) by substituting Q∗ into the profit function. In this case, we can multiply the value of π(Q∗) by 9 to obtain the maximum profit level (π∗).
Learn more about relative maximum point here:
https://brainly.com/question/32310828
#SPJ11
what’s the company’s profit if each sign sold is $20?

Answers
Answer:
what’s the company’s profit if each sign sold is $20?
Acceleration Worksheet:
Could anyone complete with correct answers? 1-5 please!

Answers
It would be negative because your subracting
What do you call a CAD software?

Answers
Answer:
Computer Aided Design
Step-by-step explanation:
CAD is Computer Aided Design
OR
CADD is Computer Aided Design and Drafting
Answer:
The last one:
Computer Aided Design
identify the values of a h and k y=5/x+6-2

Answers
The values of a, h and k on the function are given as follows:
a = 5.h = 6.k = -2.The meaning of the transformations is given as follows:
Multiplication by a = 5 -> vertical stretch by a factor of 5.h = 6 -> translation left 6 units.k = -2, translation down 2 units.What is a translation?A translation happens when either a figure or a function is moved horizontally or vertically on the coordinate plane.
The four translation rules for functions are defined as follows:
Translation left a units: f(x + a).Translation right a units: f(x - a).Translation up a units: f(x) + a.Translation down a units: f(x) - a.The parent function in this problem is given as follows:
y = 1/x.
Hence the meaning of the transformations is given as follows:
Multiplication by a = 5 -> vertical stretch by a factor of 5.h = 6 -> transformation f(x + 6), translation left 6 units.k = -2, transformation f(x) - 2, shift down 2 units.More can be learned about translations at brainly.com/question/28174785
#SPJ1
There are 950 students at a high school. There are 275 freshmen and 320 sophomores. What is the ratio of freshmen to sophomores in simplest form?
Answers
Answer:
55/64
Step-by-step explanation:
I used my calculator but... u can divide each number by 5.
275/5 = 55
320/5 = 64
Hope this helps! Mark as brainliest PLEASE! :)))
a closed rectangular box with a square base and volume 12 cubic feet is to be constructed using two different types of materials. the top is made of metal costing $2 per square foot, and the remaining sides and the base are made of wood costing $1 per square foot. find the dimensions of the box that minimizes the cost of construction.
Answers
The dimensions of the box that minimize the cost of construction are a square base with side length of 2 feet and a height of 3 feet.
Let's denote the side length of the square base as x and the height as h. Since the volume of the box is 12 cubic feet, we have the equation \(x^{2}\) × h = 12.
To minimize the cost of construction, we need to minimize the total cost of the materials used. The cost of the metal top is $2 per square foot, and the cost of the wood for the remaining sides and the base is $1 per square foot.
The cost C can be expressed as C = 2A + 5S, where A is the area of the top and S is the total area of the sides and the base.
The area of the top is A = x^2, and the area of the sides and the base is S = x^2 + 4xh.
Substituting these expressions into the cost equation, we have C = 2x^2 + 5(x^2 + 4xh).
Using the volume equation \(x^{2}\) ×h = 12, we can express h in terms of x: h = 12/\(x^{2}\)
Substituting this into the cost equation, we get \(C = 2x^2 + 5(x^2 + 4x(12/x^2)).\)
Simplifying further, we have C = \(2x^2 + 5(x^2 + 48/x).\)
To find the dimensions that minimize the cost, we take the derivative of C with respect to x, set it equal to zero, and solve for x. The critical point occurs at x = 2.
Substituting x = 2 back into the volume equation, we find h = 3.
Learn more about total cost here:
https://brainly.com/question/30355738
#SPJ11
need help with math

Answers
3) x=3
There are 5000 words in some story. The word "the" occurs 254 times, and the word "States" occurs 92 times. Suppose that a word is selected at random from the U.S. Constitution. (a) What is the probability that the word "States"? () (b) What is the probability that the word is "the" or "States"? () (c) What is the probability that the word is neither "the" nor "States"? ()
Answers
The probability of selecting the word "States" is about 1.84%, the probability of selecting either "the" or "States" is about 6.92%, and the probability of selecting a word that is neither "the" nor "States" is about 93.08%.
(a) The probability of selecting the word "States" from the story is determined by dividing the number of occurrences of "States" by the total number of words in the story. In this case, the probability is 92/5000, which simplifies to 0.0184 or 1.84%. (b) To find the probability of selecting either "the" or "States," add the individual probabilities of each word. The probability of "the" is 254/5000 or 0.0508 (5.08%), and we already calculated the probability of "States" as 1.84%. The combined probability is 0.0508 + 0.0184 = 0.0692, or 6.92%. (c) To determine the probability of selecting a word that is neither "the" nor "States," subtract the combined probability of selecting either of those words from 1. The probability of selecting neither "the" nor "States" is 1 - 0.0692 = 0.9308, or 93.08%.
To know more about probability visit :-
https://brainly.com/question/22983072?
#SPJ11
What should be done to solve the equation?
X- 17 = 11
Add 17 to both sides.
Add 17 to the left side and subtract 11 from the right side.
Add 17 to the left side and subtract 17 from the right side.
Add 11 to both sides.
Answers
Answer:
add 17 to both sides
Step-by-step explanation:
as it cancels itself
mark brainliest
Answer:
Add 17 to both sides
Step-by-step explanation:
i did the quiz
or the circle below, find the equation that represents that circle.

Answers
The general form for the equation of a circle is given by:
\((x-x_0)^2+(y-y_0)^2=r^2...(1)\)Where (x₀, y₀) are the coordinates of the center, and r is the radius. From the problem, we identify:
\(\begin{gathered} (x_0,y_0)=(1,0) \\ r=3 \end{gathered}\)Finally, using (1):
\(\begin{gathered} (x-1)^2+(y-0)^2=3^2 \\ \\ \therefore(x-1)^2+y^2=9 \end{gathered}\)Help! Please, kinda hard

Answers
Answer: −8.68n−6.8
Step-by-step explanation: To find the opposite of 4+14.3n, find the opposite of each term. 5.62n−2.8−4−14.3n. Subtract 4 from −2.8 to get −6.8. 5.62n−6.8−14.3n. Combine 5.62n and −14.3n to get −8.68n. −8.68n−6.8.
Answer: the answer is -8.68n-68
Step-by-step explanation:
Scarlet regularly works a 40 hour work week and earns $9 per hour. She receives time and a half pay for each hour of overtime that she works. Last vieek, she worked 43 hours. 1. What was her regular gross pay? 2. What was her overtime pay? 3. What was her total pay for the week? John's veekly salary is $478.25. His employer is changing the pay period to semimonthly. 4. What is his annual salary? 5. What vill his semimonthly salary be to the nearest cent?
Answers
1. Regular Gross Pay: $360 2.Overtime Pay: $40.50 3.Total Pay for the Week: $400.5 4. Annual Salary: $11,478
5. Semi-Monthly Salary: $478.25.
Here are the solutions to the given problems:
1. Regular Gross PayScarlet worked a 40-hour week at $9 per hour.
Regular gross pay of Scarlet= $9 × 40= $360
2. Overtime PayScarlet worked 43 hours in total but 40 hours of the week is paid as regular.
So, she has worked 43 - 40= 3 hours as overtime. Scarlet receives time and a half pay for each hour of overtime that she works. Therefore, overtime pay of Scarlet= $9 × 1.5 × 3= $40.5 or $40.50
3.Total Pay for the Week The total pay of Scarlet for the week is the sum of her regular gross pay and overtime pay.
Total pay of Scarlet for the week= $360 + $40.5= $400.5
4. Annual SalaryJohn's weekly salary is $478.25.
There are two pay periods in a month, so he will receive his salary twice in a month.
Total earnings of John in a month= $478.25 × 2= $956.5 Annual salary of John= $956.5 × 12= $11,478
5. Semi-Monthly SalaryJohn's semi-monthly salary is his annual salary divided by 24, since there are two semi-monthly pay periods in a year. Semi-monthly salary of John= $11,478/24= $478.25.
To know more about Regular Gross visit:
brainly.com/question/29097397
#SPJ11
What is the positive solution to this equation?
4x2 + 12 x= 135
Answers

URGENT PLEASE HELP ME I SUCK AT GEO

Answers
Answer: 225°
Step-by-step explanation:
Each rotation is 45°
From C to H, there are five rotations
5 * 45 = 225°
Answer:
D: 225 degrees
Step-by-step explanation:
You want to first find the value of each angle that comes in together at point P. To do this, you take 360 degrees/8 degrees. 360 since that is a central angle and 8 because there are 8 congruent angles that make up the central angle. You should get 45 degrees. Then since it takes 5 "45 degree turns" to get onto H, you would do 5 times 45 to get 225.
Write the expanded form of 5(2a+b -6)
Answers
Answer:
10a+5b-30
Step-by-step explanation:
Apply the distributive law = ma + mb + mc
5 (2a+b-6) = 5 2a + 5b + 5 (-6)
Then Simplify: 5 2a + 5b + 5 (-6)
= 10a+5b-30
Hope this helps :D
12. If ATSR-ATFE, find the perimeter of ATFE.
E-M
R
F
40
54
T
25
22
S

Answers
Step-by-step explanation:
they are similar, that means for our case here that they're is one central scaling factor for all sides between the 2 triangles.
by looking at the forms of both triangles, we see that
ET corresponds to TR.
FT corresponds to TS.
FE corresponds to RS.
for TE and TR we have the length information :
25 and 40
so, the scaling factor between these 2 corresponding sides can then be used for the other pairs of corresponding sides.
the scaling factor to go from the large to the small triangle is
25/40 = 5/8
therefore,
FT = TS × 5/8 = 22 × 5/8 = 11×5/4 = 55/4 = 13.75
FE = RS × 5/8 = 54 × 5/8 = 27×5/4 = 33.75
the perimeter of TFE is therefore
25 + 13.75 + 33.75 = 72.5
Write an equation in slope-intercept form that describes that data in the table

Answers
From the data points given the linear equation in slope-intercept form is y = -1/2x + 4.
What is an equation?
A mathematical definition of an equation is a claim that two expressions are equal when they are joined by the equals sign ("=").
The first two data points are - (-3,5.5) and (-1,4.5)
The slope-intercept form of the equation is -
y = mx + b
m represents the slope of the linear equation.
To find the value of m use the formula -
(y2 - y1)/(x2 - x1)
Substitute the values into the equation -
(4.5 - 5.5)/[(-1) - (-3)]
Use the arithmetic operation of subtraction -
(-1)/(-1 + 3)
-1 / 2
So, the slope m is m = -1/2
Now, the equation becomes y = -1/2x + b
To find the value of b substitute the values of x and y in the equation -
5.5 = -1/2(-3) + b
5.5 = 3/2 + b
5.5 = 1.5 + b
b = 5.5 - 1.5
b = 4
So, now the equation becomes - y = -1/2x + 4
The graph for the equation is plotted.
Therefore, the equation is y = -1/2x + 4.
To learn more about equation from the given link
https://brainly.com/question/28871326
#SPJ1

a ferris wheel has five cars, each containing four seats in a row. there are 20 people ready for a ride. in how many ways can the ride begin? what if a certain two people want to sit in different cars?\
Answers
There are 5 possible ways for the ride to begin.
The ferris wheel has 5 cars with 4 seats in each car, making a total of 20 seats. If there are 20 people ready for the ride, then each car can have 4 people. Therefore, there are 5 possible ways for the ride to begin.
If two certain people want to sit in different cars, then there are 4^2 (4x4) combinations of cars for these two people. This gives us 16 possible ways for the ride to begin.
Learn more about Ride to begin
brainly.com/question/28565842
#SPJ11