Who is correct and why?
•A. Kevin is correct. Amy did not regroup properly.
•B. Amy is correct. Kevin did not regroup properly.
•C. Kevin is correct. Amy did not line up the decimals correctly.
•D. Amy is correct. Kevin did not line up the decimals correctly.

Answers
Answer:
the answer is D. Amy is correct. Kevin did not line up the decimals correctly.
Related Questions
Joanne and Richard volunteer at a hospital. Joanne volunteers 4 hours more per week than
Richard does. In a given week, they do not volunteer for more than a combined total of 16 hours.
If æ is the number of hours that Richard volunteers, which inequality best models this situation?

Answers
The correct inequality that represents the given scenario is, x + 4 ≤ 16. Hence option A is true.
Used the concept of inequality,
A relation by which we can compare two or more mathematical expressions is called an inequality.
Given that,
Joanne volunteers 4 hours more per week than Richard does.
In a given week, they do not volunteer for more than a combined total of 16 hours.
Let x be the number of hours that Richard volunteers.
Then the correct inequality is,
x + 4 ≤ 16
Therefore, option A is true.,
To learn more about inequality visit:
https://brainly.com/question/25944814
#SPJ4
help solve this for me pls

Answers
Answer:
x ( > or = ) 5/9
Step-by-step explanation:
● 2(1 + x) ( > or = ) 11 - 3x
● 2 + 2x ( > or = ) 11 - 3x
Add 3x to both sides
● 2 + 2x + 3x ( > or = ) 11 - 3x + 3x
● 2 + 5x (> or = ) 11
Substract 2 from both sides
● 2 + 5x -2 ( > or = ) 11 -2
● 5x (> or =) 9
Divide both sides by 5
● 5x/5 ( > or = ) 5/9
● x ( > or = ) 5/9
Causes of variation that can be identified and eliminated are called what?
Answers
The causes of variation that can be identified and eliminated are called; Assignable Causes.
What are the causes of Variation?There are two primary causes of variation in the quality of a product or process. These two primary causes are called;
Common causes.Assignable causes.Now, Common causes of variation are defined as random causes that we cannot identify. However, Assignable causes of variation are those that can be identified and eliminated.
Read more about Variation Causes at; https://brainly.com/question/14926046
#SPJ1
(x-9)(×+4)=168 solve for xI just need reminded how to do the x-9 * x+4 please
Answers
The given expression is
\((x-9)(x+4)=168\)To solve the product, we have to use the distributive property
\(x^2+4x-9x-36=168\)Then, we move all the terms to the left side to combine like terms
\(\begin{gathered} x^2+4x-9x-36-168=0 \\ x^2-5x-204=0 \end{gathered}\)Now, we use the quadratic formula to find the solutions
\(x_{1,2}=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}\)Where a = 1, b = -5, and c = -204. Let's replace these values
\(\begin{gathered} x_{1,2}=\frac{-(-5)\pm\sqrt[]{(-5)^2-4(1)(-204)}}{2(1)} \\ x_{1,2}=\frac{5\pm\sqrt[]{25+816}}{2}=\frac{5\pm\sqrt[]{841}}{2} \\ x_{1,2}=\frac{5\pm29}{2} \end{gathered}\)There are two solutions
\(\begin{gathered} x_1=\frac{5+29}{2}=\frac{34}{2}=17 \\ x_2=\frac{5-29}{2}=\frac{-24}{2}=-12 \end{gathered}\)Hence, the solutions are x = 17, and x = -12.The point A has coordinates (5, -4)
The point B has coordinates (13, 1)
a) Work out the coordinates of the midpoint of AB.
Line L has equation y = 2 - 3x
b) Write down the gradient of Line L.
Line L has equation y = 2 - 3x
c) Does the point with coordinates (100, -302) lie on line L?
You must give a reason for your answer.
Answers
The midpoint of AB has coordinates (9, -1.5), the gradient of line L is -3 and the point (100, -302) doesn't lie on L.
What is a coordinate?
Coordinates are numerical lengths or angles that uniquely identify locations on two-dimensional (2D) surfaces or in three-dimensional (3D) space (3D). Mathematicians, physicists, and engineers employ a variety of coordinate schemes.
(a) Given point A (5, -4) and point B (13, 1)
Therefore, midpoint of AB is \((\frac{x1+x2}{2},\frac{y1+y2}{2})\)
\(or,(\frac{5+13}{2},\frac{-4+1}{2})\)
\(or, (\frac{18}{2},\frac{-3}{2} )\)
\(or,(9, -1.5)\)
(b) In the equation \(y=2-3x\), -3 is the gradient of line L.
(c) The point with coordinates (100, -302) doesn't lie on L as it doesn't satisfy the equation \(y=2-3x\)
To know more about coordinates, click on the link
https://brainly.com/question/18269861
#SPJ1
If the measure of two sides of the triangle are 3 feet's and 7 feet's, which is the least possible whole number measure for the third side
Answers
Answer:
5 feet
Step-by-step explanation:
By triangle inequality, the sum of lengths of any two sides has to be strictly greater than the length of the third side.
Let x feet be the length of the third side.
We have 3+x>7, x+7>3 and 3+7>x.
Solving these, we get x > 4, x > -4 and x < 10.
The solution is therefore 4 < x < 10 and the smallest whole number which satisfies the inequality is 5.
Therefore the answer is 5 feet.
If you deposit or put in $1550 into a savings account earning 7.2% simple interest for 2 years, how much money total will you have in your account? Show the equation you use and solve.
Answers
Answer:
22320
Step-by-step explanation:
simple interest= p (deposit) × r (rate) × t (time)
=1550×7.2×2
=22320
The volume of an oblique pyramid with a square base is V units3 and the height is h units.
An oblique pyramid with a square base has a volume of V units cubed and a height of h units.
Which expression represents the area of the base of the pyramid?
StartFraction 3 V Over h EndFraction units2
(3V – h) units2
(V – 3h) units2
StartFraction V Over 3 h EndFraction units2
Answers
Answer:
StartFraction 3 V Over h EndFraction units2Step-by-step explanation:
volume of an oblique square pyramid V = 1/3 * b * H where;
b is the base area of the pyramid
H is the height of the pyramid
To determine the expression that represents area of the base of the pyramid, we will make the variable 'b' the subject of the formula from
V = 1/3 bH
\(V=\frac{bH}{3}\)
Cross multiplying we have;
\(3V = bH\\\)
Dividing both sides by H we have;
\(\frac{3V}{H} = \frac{bH}{H} \\b = \frac{3V}{H}units^{2}\)
This gives the correct expression for the base area of the pyramid
Answer:
A.
Step-by-step explanation:
A mango tree casts a shadow that is 8 m long. If the tree is 17 m high, what is the
angle of elevation of the sun?
The angle of depression of a car from the top of a 125-ft tower is 29°. How far is
the car from the tower's base?
A 4-m stick leans against a wall and the base of the stick is 2 m from the base of
the wall. What is the angle of elevation of the stick?
At a particular time when the angle of elevation of the sun is 49°, a flagpole casts
a shadow that is 4 m long. How high is the flagpole?
The angle of depression of a boat from the top of a lighthouse is 38°. What is the
height of the lighthouse given that the distance from the boat to the foot of the
lighthouse is 255 ft?
Answers
Using the slope concept, it is found that:
The angle of elevation of the sun is of 64.8º.The car is 225.5 ft from the tower's base.The angle of elevation of the stick is of 63.4º.The flagpole has a height of 4.6m.The lighthouse has a height of 199 ft.What is a slope?The slope is given by the vertical change divided by the horizontal change, and it's also the tangent of the angle of depression.
Hence, for the mango tree, we have that:
tan(x) = 17/8
x = arctan(17/8)
x = 64.8º.
Which is the angle of elevation of the sun.
For the car, we have that:
tan(29º) = 125/d
d = 125/tan(29º)
d = 225.5.
Which is the distance.
For the stick, we have that:
tan(x) = 4/2
x = arctan(2)
x = 63.4º.
Which is the angle of elevation of the stick.
For the flagpole, we have that:
tan(49º) = h/4.
h = 4 x tan(49)
h = 4.6 m.
Which is the height of the flagpole.
For the lighthouse, we have that:
tan(38) = h/255.
h = 255 x tan(38)
h = 199 ft.
Which is the height of the lighthouse.
More can be learned about the slope concept at https://brainly.com/question/18090623
#SPJ1
A recipe requires 34 cups of milk. Paula is making 12 of the recipe. How many cups of milk will Paula use?
Answers
find the average value of the following function over the given interrval. draw a graph of the funciton and indivicate the average value. f(x) = x(x-1); [2,7]
Answers
17.83 is the average value of the function f(x) = x(x-1) over the interval [2, 7]
To find the average value of the function f(x) = x(x-1) over the interval [2, 7], we need to calculate the definite integral of the function over that interval and divide it by the width of the interval.
First, let's find the definite integral of the function f(x) = x(x-1):
∫[2, 7] x(x-1) dx
Integrating the function, we get:
∫[2, 7] (x^2 - x) dx = [1/3 x^3 - 1/2 x^2] evaluated from 2 to 7
Plugging in the upper and lower limits, we get:
\([1/3 (7)^3 - 1/2 (7)^2] - [1/3 (2)^3 - 1/2 (2)^2]\)
= [1/3 (343) - 1/2 (49)] - [1/3 (8) - 1/2 (4)]
Simplifying further, we have:
= (343/3 - 49/2) - (8/3 - 6/3)
= (539/6) - (2/3)
= (539/6) - (4/6)
= 535/6
Now, to find the average value, we divide the definite integral by the width of the interval:
Average value = (535/6) / (7 - 2)
= (535/6) / 5
= 535/30
= 17.83
Therefore, the average value of the function f(x) = x(x-1) over the interval [2, 7] is approximately 17.83.
Learn more about function here:
https://brainly.com/question/29633660
#SPJ1
plsssssssssss help me

Answers
Answer: 40
Step-by-step explanation:
38+ 52=90
230-90=40
The height of a plant, y, in centimeters, is measured x weeks after planting a seed. The height can be modeled by the regression equation y = StartFraction 6.88 Over 1 + 2,139.99 e Superscript negative 0.47 x Baseline EndFraction. Which statement best interprets the value 6.88? The plant grows 6.88 cm each week. The initial height of the plant is 6.88 cm. The plant takes 6.88 weeks to reach a height of 2,139.99 cm. The limiting value for the height of the plant is 6.88 cm.
Answers
After 7 weeks, the plant's approximate height is 8.7 cm.
What is equation?An equation is a formula in mathematics that expresses the equivalence of two expressions by linking them with the equals symbol =. In its most basic form, an equation is a mathematical statement that indicates that two mathematical expressions are equal. 3x + 5 = 14, for example, is an equation in which 3x + 5 and 14 are two expressions separated by a 'equal' sign. A mathematical equation that depicts the connection between two expressions on opposite sides of the sign. It generally consists of one variable and one equal to symbol.
Here,
You are given a a graph titled Plant Height that shows Number of Weeks on x axis and Height of Plant in cm on y axis. Plotting this and you will get an equation of y = 1.2792x - 0.1665 (I used excel using the given points from the above problem).
y = 1.2792x - 0.1665
y = 1.2792 (7) - 0.1665
y = 8.78 centimeters.
The most likely approximate height of the plant after 7 weeks is 8.7 centimeters.
To know more about equation,
https://brainly.com/question/4449615
#SPJ1
if the volume of a ball is 32,490 cubic millimeters, what is the volume of the ball in cubic centimeters?
Answers
The volume of ball is 32.49 cubic centimeter.
What is volume ?
Every three-dimensional item takes up space in some way. The volume of this area is what is used to describe it. The area occupied within an object's three-dimensional bounds is referred to as its volume. The object's capacity is another name for it.
Here ,
The volume of a ball = 32490 cubic millimeters
To convert into cubic millimeter into cubic centimeter by dividing by 1000, Then,
=> 32490/1000
=> 32.49 cubic centimeter.
Hence the volume of ball in cubic centimeter is 32.49 .
To learn more about volume
https://brainly.com/question/14197390
#SPJ4
The store opened at 8:15 a.m. and closed at 11:45 p.m. how long was the store opened?
Answers
Answer:
3 hours and 30 minutes
Step-by-step explanation:
8:15+3=11:15
11:15+30=11:45
Answer:
15 hr 30 min
Step-by-step explanation:
8:15 - 9 am = 45 min
9 am to 11 pm = 14 hours
11pm - 11:45 pm = 45 min
90 min = 1 hr 30 min
14 hr + 1 hr 30 min = 15 hr 30 min
Find the t values that form the boundaries of the critical region for a two-tailed test with a = 0.05 for each of the following df values. a) df = 8 b) df = 15 c) df = 24
Answers
The boundaries of the critical region for a two-tailed test with a = 0.05 for each of the following df values are given below:a) df = 8 : t = ±2.306b) df = 15 : t = ±2.131c) df = 24 : t = ±2.064
The critical value of t is determined by the degrees of freedom (df) and the level of significance (α) for a two-tailed test.
When the level of significance is 0.05, the critical value of t is used to define the boundaries of the critical region.
The null hypothesis is accepted if the test statistic falls within the critical region, while the alternative hypothesis is accepted if it falls outside the critical region.
For the degrees of freedom (df) 8, the critical values of t are ±2.306. For df = 15, the critical values of t are ±2.131. And for df = 24, the critical values of t are ±2.064.
These values are calculated using a t-distribution table or statistical software like SPSS.
By comparing the calculated test statistic with the critical values of t, we can decide whether to accept or reject the null hypothesis.
If the test statistic is greater than the positive critical value or less than the negative critical value, we reject the null hypothesis.
If the test statistic is between the positive and negative critical values, we fail to reject the null hypothesis.
In conclusion, we can find the critical values of t for a two-tailed test with a = 0.05 by using a t-distribution table or statistical software, given the degrees of freedom.
To know more about null hypothesis visit:
brainly.com/question/30821298
#SPJ11
Which meaning of multiplication does the following problem repre
Taylor has 5 baskets. There are 6 balls in each basket. How many balls does she have?
A) Groups of
B) Area / Array
C) Fundamental Counting Theorem
D) Fractional Part of a Number
Answers
Given problem represent Fundamental Counting Theorem.
Fundamental Counting Theorem states that if an event can occur in m different ways, and another event can occur in n different ways, then the total number of occurrences of the events is m×n.
Here Taylor has 5 baskets and there are 6 balls in each basket.
That is m = 5 and n = 6
Therefore Taylor have m×n= 5×6 =30 balls
Hence here we use Fundamental counting theorem.
To know more about Fundamental counting theorem here
https://brainly.com/question/16025130
#SPJ1
please this for me I don’t get it :/

Answers
Answer:
x = 3
Step-by-step explanation:
-5x + 10 = -5
-10 -10
-5x = -15
divide by -5
x = 3
Answer:
\(x = 11\)
Step-by-step explanation:
\( - 5(x - 10) = - 5\)
\( - 5 \times x - 10 \times - 5 = - 5\)
\( - 5x + 50 = - 5\)
\( - 5x = - 5 - 50\)
\( - 5x = - 55\)
\( \frac{ - 5x}{ - 5} = \frac{ - 55}{ - 5} \)
\(x = 11\)
\( - 5(11 - 10) { = }^{?} - 5\)
\( - 5 \times 11 - 5 \times - 10 { = }^{?} - 5\)
\( - 55 + 50 { = }^{?} - 5\)
\( - 5 = - 5\)
The principal at Key North Middle School wants to determine if the 85 students in the seventh grade prefer to collect bottles or sell magazines as their yearly fundraiser. Which of the following is a set of people that could be a representative sample of the population?
Answers
Using sampling concepts, it is found that a sample that involves an equal proportion of boys and girls is representative of the population.
What is sampling?It is a common statistics practice, when we want to study something from a population, we find a sample of this population, which is a group containing elements of a population. A sample has to be representative of the population, that is, it has to involve all segments of the population.
The students of the seventh grade can be divided into boys and girls, hence, a sample that involves an equal proportion of boys and girls is representative of the population.
More can be learned about sampling concepts at https://brainly.com/question/25122507
Find all solutions of sin x - square 3-3 sin^2x=0
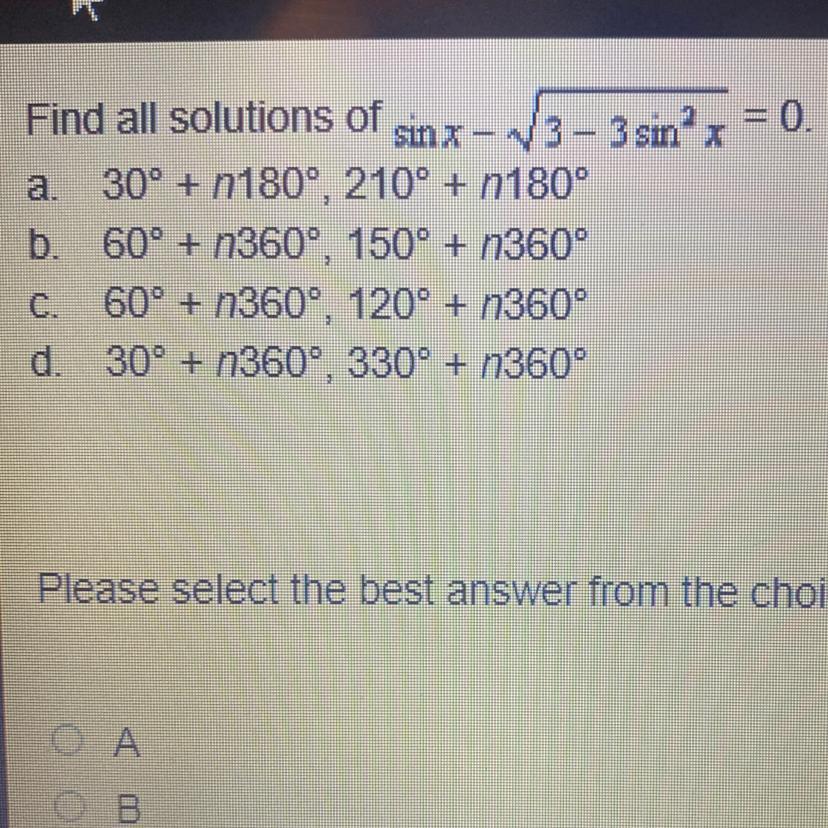
Answers
Answer:
C) \(60^\circ+n360^\circ,120^\circ+n360^\circ\)
Step-by-step explanation:
\(sinx-\sqrt{3-3sin^2x}=0\)
\(sinx=\sqrt{3-3sin^2x} \)
\(sin^2x=3-3sin^2x\)
\(4sin^2x=3\)
\(sin^2x=\frac{3}{4} \)
\(sinx=\pm\sqrt{\frac{3}{4} } \)
\(sinx=\pm\frac{\sqrt{3}}{2} \)
\(x=\frac{\pi}{3}+2\pi n,\frac{2\pi}{3}+2\pi n \)
\(x=60^\circ+n360^\circ,120^\circ+n360^\circ\)
Therefore, the correct option is C
what is the domain and range?

Answers
Answer:
\(Dom= R-\{-4\}\)
\(Range = R- \{0\}\)
Step-by-step explanation:
Mabel ate dinner at a restaurant.The bill came to $79.If she left a 20% tip,how much was the tip?
Answers
The declaration made indicates that Mabel left a $15.80 gratuity.
How do the percentages translate?Percent, which is a relative number used to denote hundredths of any amount. Since one percent is equal to one tenth of something, 100 percent stands for everything, and 200 percent refers to twice the amount specified. percentage.
To find the amount of the tip that Mabel left, we can multiply the bill amount by the tip percentage, which is 20% or 0.2 in decimal form.
The amount of the tip is:
Tip = Bill Amount x Tip Percentage
Tip = $79 x 0.2
Tip = $15.80
Therefore, the tip that Mabel left was $15.80.
To know more about Percentage visit:
https://brainly.com/question/24877689
#SPJ1
Need help with number 21

Answers
value of x is 11.
hope this answer helps you dear....take care and may u have a great day ahead!

h(x) = 4x +3. What is
the coordinate pair for h (1)?
Answers
9514 1404 393
Answer:
(1, 7)
Step-by-step explanation:
Fill in x=1 and do the arithmetic.
h(1) = 4(1) +3 = 7
The coordinate pair is ...
(x, h(x)) = (1, h(1)) = (1, 7)
If x = 2, y = 3 and z = 4, calculate the value of each of the following algebraic expression: 3x + 3y =
Answers
3(2) + 3(3)
6 + 9
15
One model for the spread of a rumor is that the rate of spread is proportional to the product of the fraction y of the population who have heard the rumor and the fraction who have not heard the rumor. (a) Write a differential equation that is satisfied by y. (Use k for the constant of proportionality.)
dy/dt = ____
(b) Solve the differential equation. Assume y(0) = C. y = _____
(c) A small town has 1300 inhabitants. At 8 AM, 100 people have heard a rumor. By noon half the town has heard it. At what time will 90% of the population have heard the rumor? (Do not round k in your calculation. Round the final answer to one decimal place.) ______hours after the beginning
Answers
(a) The differential equation that is satisfied by y is:
\(\frac{dy}{dt} = ky(1-y)\)
(b) To solve the differential equation, we separate the variables and integrate both sides:
\(\frac{dy}{y*(1-y)} = k*dt\)
Integrating both sides, we get:
\(\frac{lnly}{1-y} = k*t +c1\)
where C1 is an arbitrary constant of integration.
We can rewrite the equation in terms of y:
\(\frac{y}{1-y} = e^{(k*t+c1)}\)
Multiplying both sides by (1-y), we get:
\({y} = e^{(k*t+c1)} *(1-y)\)
\(y= \frac{C}{(1+(c-1)e^{-kt} }\)
where C = y(0) is the initial fraction of the population who have heard the rumor.
(c) In this case, the initial fraction of the population who have heard the rumor is y(0) = \(\frac{100}{1300}\) = 0.077. At noon, half the town has heard the rumor, so y(4) = 0.5.
Substituting these values into the equation from part (b), we get:
\(0.5= \frac{0.077}{1+(0.777-1) e^{-k4} }\)
Solving for k, we get:
\(k= ln(\frac{12.857}{4} )\)
Substituting this value of k into the equation from part (b), and setting y = 0.9 (since we want to find the time at which 90% of the population has heard the rumor), we get:
\(0.9= \frac{0.077}{1+(0.777-1) e^{-ln(12.857}*\frac{t}{4} }\))
Solving for t, we get:
t = 8.7 hours after the beginning (rounded to one decimal place)
A differential equation is a mathematical equation that relates a function to its derivatives. It is a powerful tool used in many fields of science and engineering to describe how physical systems change over time. The equation typically includes the independent variable (such as time) and one or more derivatives of the dependent variable (such as position, velocity, or temperature).
Differential equations can be classified based on their order, which refers to the highest derivative present in the equation, and their linearity, which determines whether the equation is a linear combination of the dependent variable and its derivatives. Solving a differential equation involves finding a function that satisfies the equation. This can be done analytically or numerically, depending on the complexity of the equation and the available tools.
To learn more about Differential equation visit here:
brainly.com/question/14620493
#SPJ4
Use absolute value to express the distance between -12 and -15 on the number line
Answers>>
A. |-12-(-15)|= -27
B. |-12 - (15)|= -3
C. |-12 - (-15)|=3
D. |-12 - (15)|= 27

Answers
Answer:
C. -12-(-15) =3
Step-by-step explanation:
you subtract the two numbers to get the distance.
What is the equation of the function that is graphed as line a?
O y= 2 x-1
O y=-x-1
O y=-x
O y=3 x
please awnser quick :)

Answers
to get the equation of any straight line we simply need two points off of it, hmmm let's use the points in the picture below for "a".
\((\stackrel{x_1}{-4}~,~\stackrel{y_1}{3})\qquad (\stackrel{x_2}{2}~,~\stackrel{y_2}{-3}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{-3}-\stackrel{y1}{3}}}{\underset{run} {\underset{x_2}{2}-\underset{x_1}{(-4)}}}\implies \cfrac{-6}{2+4}\implies \cfrac{-6}{6}\implies -1\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{3}=\stackrel{m}{-1}(x-\stackrel{x_1}{(-4)}) \\\\\\ y-3=-1(x+4)\implies y-3=-x-4\implies y=-x-1\)

The length of the major axis of the ellipse below is 10 What is the sum of the lengths of the red and blue line segments? A. 10 B. 5 C. 15 D. 20
Answers
Answer:
A. 10
Step-by-step explanation:
As we know that
The length of the major axis of the ellipse is 10
i.e
2 a = 10
Also, the ellipse is the curve that consists of 2 focal points in order that the total of the distance to the 2 focal points would remain constant for each and every point displayed in the curve
Now we assume that P is the curve point
So,
PF1 + PF2
i.e
2 a (blue line) + (red line)
2 a = 10
Therefore the sum of the length is 10
Answer:
10
Step-by-step explanation:
Find the first three terms of the sequence below. Tn=n2+2n+9
Answers
\(\\ \bull\tt\longrightarrow T_n=n^2+2n+9\)
\(\\ \bull\tt\longrightarrow T_1=1^2+2(1)+9=1+2+9=12\)
\(\\ \bull\tt\longrightarrow T_2=2^2+2(2)+9=4+4+9=17\)
\(\\ \bull\tt\longrightarrow T_3=3^2+2(3)+9=9+6+9=24\)