You have $4.75 in change in your pocket. You have a total of 34 nickels, dimes and quarters. If you have one more quarter than nickels how many of each kind of coin do you have? This is for matrics and solving systems.
Answers
Solution
let n represents nickel
let d represents dimes
let q represents quarters
Related Questions
A football club is the only one in its region and is therefore able to behave like a monopolist. It sells tickets to Adults (a) and Juniors (j), whose demand curves are given by:
Pa = 200 − Qa
Pj = 160 − Qj
Additionally, the club’s total costs are given by = 20Qi
The club hires an economist to consider its pricing strategy and receives the advice that it should charge different prices to each type of supporter. Find the prices it sets in both markets, the sales (output) in each and its overall level of profit and illustrate profit maximising outputs and prices of each consumer type on a graph (one graph for each type of consumer). Calculate consumer surplus in this case.
Answers
Answer:
Adult market
price: 110sales: 9900profit: 8100consumer surplus: 9000Junior market
price: 90sales: 6300profit: 4900consumer surplus: 5600Total profit: 13000
Total consumer surplus: 14600
Step-by-step explanation:
Given Adult (a) and Junior (j) demand equations Pa = 200 -Qa and Pj = 160 -Qj, and cost equation C = 20Q, you want to find the price in each market that maximizes profit, the sales in each market, and the consumer surplus, and a graph of profit-maximizing sales and prices.
RevenueEach demand equation is of the form P = Pmax -Q, where P is the price that will result in sales of Q tickets. The revenue (R) in each case is the product of numbers of tickets sold (Q) and the price at which they are sold (P).
R = QP = Q(Pmax -Q)
ProfitThe profit is the difference between revenue and cost.
Profit = R - C = Q(Pmax -Q) -20Q
Profit = Q(Pmax -20 -Q)
Writing the demand equation in terms of P, we find ...
Q = Pmax -P
Substituting this into the Profit equation gives ...
Profit = (Pmax -P)(Pmax -20 -(Pmax -P))
Profit = (Pmax -P)(P -20)
The profit function describes a downward-opening parabolic curve with zeros at P=Pmax and P=20. The maximum profit is on the line of symmetry of this curve, halfway between these values of P:
Price for maximum profit = (Pmax +20)/2 = Pmax/2 +10
PricesIn the adult market, Pmax = 200, so the profit-maximizing ticket price is ...
Pa = 200/2 +10 = 110 . . . . price for maximum profit in Adult market
In the Junior market, Pmax = 160, so the profit-maximizing ticket price is ...
Pj = 160/2 +10 = 90 . . . . price for maximum profit in Junior market
SalesUsing the revenue equation, we find the sales in each market to be ...
Qa = 200 -Pa = 200 -110 = 90
Ra = Qa·Pa = 90(110) = 9900 . . . . sales in Adult market
Qj = 160 -Pj = 160 -90 = 70
Rj = Qj·Pj = 70(90) = 6300 . . . . sales in Junior market
Overall ProfitThe profit in each market is ...
Adult market profit = 90(110 -20) = 8100
Junior market profit = 70(90 -20) = 4900
The overall profit will be the sum of the profits in each market:
Overall profit = 8100 +4900 = 13000
Consumer surplusThe consumer surplus in each market is the area below the demand curve and above the price point. It is half the product of the maximum price and the quantity actually sold.
CSa = (1/2)(200)Qa = 100(90) = 9000
CSj = (1/2)(160)(Qj) = 80(70) = 5600
The total consumer surplus is ...
CS = CSa +CSj = 9000 +5600 = 14,600 . . . . total consumer surplus
Graph
The first attachment shows the sales (output) in each market (red=Adult, purple=Junior) as a function of ticket price. It also shows the corresponding profit (orange=Adult, blue=Junior). The profit-maximizing price point is marked on each curve. You will note that it is different from the output-maximizing price point.
The second attachment illustrates the consumer surplus in each market. That graph has price on the vertical axis, and quantity on the horizontal axis. The colors correspond to the colors on the graph in the first attachment.


karla is offered a job as parking lot attendant. the job will pay 2400 per month, paid biweekly. along with the base salary, the company offers to pay half the cost of medical insurance and will match karlas contribution to a retirment plan up to a total of 1500. if the full cost of the medical insurance is 450 a month and karla plans to contribute the full 1500 every year tpa retirement plan, what is the actual annual value of this job to karla?
Answers
The actual annual value of this job to Karla is 33000.
What are arithmetic operations?
Arithmetic operations is a branch of mathematics that studies numbers and the operations on numbers that are useful in all other branches of mathematics. It consists primarily of operations like addition, subtraction, multiplication, and division.
We have,
the job will pay 2400 per month,
if the full cost of the medical insurance is 450 a month and Karla plans to contribute the full 1500 every year tpa retirement plan,
the actual annual value of this job to Karla is:
2400 per month
annual value = 2400 * 12 = 28,800
the medical insurance is 450 a month
half the cost of medical insurance is 225 a month
annual value = 225 * 12 = 2700
the full 1500 every year tpa retirement plan,
So, the total value is:
= 28,800 + 2700 + 1500
= 33000
Hence, the actual annual value of this job to Karla is 33000.
To learn more about arithmetic operations visit,
brainly.com/question/4721701
#SPJ1
solve for x3(x-2)+4=28
Answers
Answer: here’s the answer!
Step-by-step explanation: hope this helps!

Answer:
x=10
Step-by-step explanation:
3(x-2)+4=28
3x-6+4=28
3x-2=28
3x=30
x=10
1.1. Thembile is a second hand dealer. She bought the sewing machine for R5700 and later sold it for R8850. 1.1.1. How much profit/loss was made? Profit selling price - cost price
Answers
The profit made from Thembile selling the second hand sewing machine if the cost price is R5700 and the selling price is R8850 is R3150.
How much profit/loss was made?Profit/loss refers to the difference between the cost price and selling price of an item. When the difference is positive; it is profit. When the difference is negative; it is loss.
Cost profit = R5700
Selling price = R8850
Profit = Selling price - Cost price
= R8850 - R5700
= R3150
Ultimately, Thembile made a profit of R3150 on the second hand sewing machine.
Read more on profit:
https://brainly.com/question/23706629
#SPJ1
If f (x) = 2 x + 5 and three-halves are inverse functions of each other and StartFraction 41
Answers
The inverse of the function → f(x) = 2x + 5 is → f⁻¹(x) = (x/2) - (5/2).
What is the procedure to find inverse of function ?Inverse of a function can be calculated by following the steps mentioned below -
Step 1 - Replace {y} with {x} and vice - versa.Step 2 - Rewrite the equation by solving for {y}.Step 3 - Replace {y} with f⁻¹(x).According to the question, the equation given is as follows
y = f(x) = 2x + 5
y = 2x + 5
Replace 'y' with 'x', we get -
x = 2y + 5
Now, solve for y -
2y = x - 5
y = (x/2) - (5/2)
Replace 'y' with f⁻¹(x) -
f⁻¹(x) = (x/2) - (5/2)
Hence, the inverse of the function → f(x) = 2x + 5 is → f⁻¹(x) = (x/2) - (5/2).
To solve more questions on inverse of function, visit the link below-
brainly.com/question/28229665
#SPJ1
What is the greatest whole number that rounds to 2,800 when rounded to the nearest hundred? The least whole number?
Answers
Answer:
The greatest is 2,799
The lowest is 2,750
Step-by-step explanation:
Answer: The greatest whole number: 2799
The least whole number: 2750
Step-by-step explanation: I just went by the rule five or more round-up.
Help me
See the picture
I’m giving brainliest

Answers
Answer: y = -x - 8
Step-by-step explanation: check the pic attached and lemme know if u dont get it :)

PLEASE SOMEONE CAN HELP WITH THIS IT HAVE TO BE DONE AND Is easy points please and thank you (sorry for screaming ).

Answers
Calculate the slope of the line joining the points (1,1) and (-3,-1).
\(\begin{gathered} m=\frac{y2-y1}{x2-x1} \\ m=\frac{-1-1}{-3-1} \\ m=0.5 \end{gathered}\)Use the equation m1m2=-1 to calculate the slope of the perpendicular line.
\(\begin{gathered} m1m2=-1 \\ m2=-\frac{1}{m1} \\ m2=-\frac{1}{0.5} \\ m2=-2 \end{gathered}\)Given that, the line passes through the point (-3,4).
Use point slope form to calculate the equation of the line.
\(\begin{gathered} y-y1=m(x-x1) \\ y-4=-2(x+3) \\ y-4=-2x-6 \\ y=-2x-2 \end{gathered}\)Therefore, the equation of the line is y=-2x-2.
A 50 foot building casts a shadow that is 65 feet long. At the same time of day, a 10 foot sign casts how long of a shadow?
Answers
50 10
___=___
65 x
50(x)=(65)(10)
50x=650
x=650/50
x=13
18% of 200 is between which two numbers?
Answers
Answer:
35&37
Step-by-step explanation:
Well 18% of 200 is 36 so...
Operations with Expressions Consider the expressions:
Expression 1: −9x + 8y
Expression 2: −8x − 2y
Question 1
Subtract expression 1 from expression 2.
Responses
A x + 6y
B x − 10y
C 10y − x
D 6y − x
Question 2
Subtract expression 2 from expression 1?
Responses
A x + 6y
B x − 10y
C 6y − x
D 10y − x
Answers
Answer:13 x
Step-by-step explanation: bc i did the test
work out the circumferrence of this circle 14cm diameter give your answer in terms of pi and state its units
Answers
Answer:
Step-by-step explanation:
The circumference of a circle is given by the formula:
C = πd
where d is the diameter of the circle. In this case, the diameter is given as 14 cm, so we can substitute that into the formula:
C = π(14 cm)
Multiplying, we get:
C = 14π cm
So the circumference of the circle is 14π cm. The units are centimeters, since circumference is a length measurement.
Graph the line. pllzzzzzzzz

Answers
Answer:
Step-by-step explanation:
X: -2, -1, 0, 1, 2,...
Y: -2, -1, 0, 1, 2,...
(y=x)

evaluate cos(sin^-1 x0)
Answers
Answer:
Pull terms out from under the radical, assuming positive real numbers.
0
Step-by-step explanation:
Please help please no links please please anything helps

Answers
Answer:
140
Step-by-step explanation:
Possibly i'm not that great at math but this might be the answer.
5t+7+8b
I need also help on -2(x+3)=_-6
Answers
The solution to the equation -2(x + 3) = -6 is x = 0.
To simplify the expression 5t + 7 + 8b, we can combine like terms.
There are two like terms in the expression: 5t and 8b.
Combining the like terms gives us:
5t + 8b + 7
Therefore, the simplified form of the expression 5t + 7 + 8b is 5t + 8b + 7.
Regarding the equation -2(x + 3) = -6:
To solve this equation, we can follow these steps:
Distribute the -2 to the terms inside the parentheses:
-2 * x + (-2) * 3 = -6
This simplifies to:
-2x - 6 = -6
Move the constant term to the right side by adding 6 to both sides of the equation:
-2x = 0
Divide both sides of the equation by -2 to isolate the variable x:
x = 0 / -2
Simplifying the right side of the equation gives us:
x = 0
The solution to the equation -2(x + 3) = -6 is x = 0.
The simplified expression 5t + 7 + 8b remains as 5t + 8b + 7, and the solution to the equation -2(x + 3) = -6 is x = 0.
For more questions on equation
https://brainly.com/question/17145398
#SPJ8
A rancher has 200 feet of fencing to enclose two adjacent rectangular corrals. What dimensions should
be used so that the enclosed area will be a maximum?
Answers
Length is 33.33 feet and width is 25 feet are dimensions should
be used so that the enclosed area will be a maximum.
What is Area of Rectangle?The area of Rectangle is length times of width
Given that, a rancher has 200 feet of fencing to enclose two adjacent rectangular corrals of the same dimensions.
Here, the dimensions of the rectangles are the same.
The width of the two rectangles is W=2W+2W=4W
The length of the two rectangles is L=L+L+L=3L
Because the adjacent side has a common length.
3L+4W=200
3L=200-4W
Divide both sides by 3
L=(200-4W)/3
Let us form an equation using the area of rectangle formula:
A=2LW
=2(200-4W)/3.W
A=400-8W²/3
Let us differentiate to get the area to be maximized dA/dW=0
1/3×(400-8W²)=0
1/3(400-16W)=0
400-16W=0
400=16W
Divide both sides by 16
W=25
The width is 25 feet.
Substitute W value in equation to get L value:
L=200-4×25/3
=200-100/3
=100/3
=33.33
The length is 33.33 feet.
Now let us find the maximum area
A=2LW
=2×33.33×25
=1666.66
Hence, length is 33.33 feet and width is 25 feet are dimensions should
be used so that the enclosed area will be a maximum.
To learn more on Rectangle click:
https://brainly.com/question/20693059
#SPJ1
PLEASE HELP ME ASAP ILL GIVE BRAINLIEST
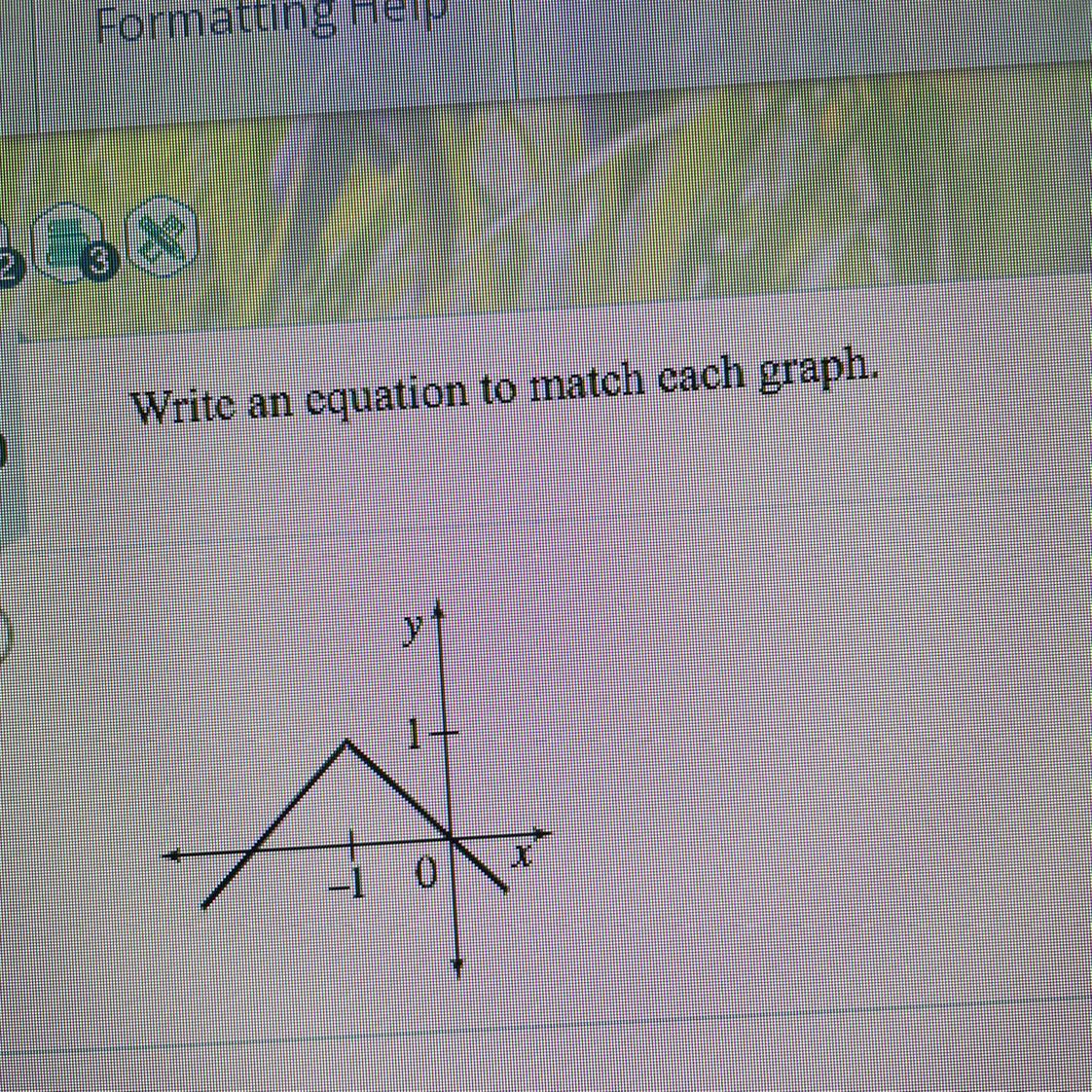
Answers
The absolute value function that matches the graph is given as follows:
y = -|x + 1| + 1.
How to define the absolute value function?An absolute value function of vertex (h,k) is defined as follows:
y = a|x - h| + k.
In which a is the leading coefficient.
The coordinates of the vertex in this problem are given as follows:
(-1, 1).
Hence:
y = a|x + 1| + 1.
The function is reflected over the x-axis with a slope of -1, hence the leading coefficient a is given as follows:
a = -1.
Thus the function is:
y = -|x + 1| + 1.
More can be learned about absolute value functions at brainly.com/question/3381225
#SPJ1
6) 1,1,3,8,19, 41
a) 60
b) 81
c) 90
d) 101
Analogias
Answers
The next term in the sequence is 98. None of the given options (60, 81, 90, 101) match the expected next term. None of the option is correct.
To find the pattern in the sequence 1, 1, 3, 8, 19, 41, we can examine the differences between consecutive terms:
1 1 3 8 19 41
0 2 5 11 22
Looking at the differences, we can observe that each subsequent difference is obtained by adding consecutive odd numbers: 2, 3, 4, 5, etc. This suggests that the original sequence may be related to square numbers.
Let's check if the differences between consecutive terms are square numbers:
2 = 1²
5 = 2² + 1²
11 = 3² + 2²
22 = 4² + 3²
Based on this pattern, we can make a reasonable assumption that the next difference should be 5² + 4² = 41 + 16 = 57. Adding this difference to the last term of the sequence (41), we get the next term:
41 + 57 = 98
Therefore, the next term in the sequence is 98. None of the given options (60, 81, 90, 101) match the expected next term.
Hence, none of the given options accurately continue the pattern of the sequence. It's important to note that patterns in sequences can sometimes have multiple possible interpretations, and it's always essential to consider alternative patterns or extend the sequence further to confirm the pattern.
For moresuch questions on sequence visit:
https://brainly.com/question/30762797
#SPJ8
In simplest radical form, what are the solutions to the quadratic equation 0 = –3^2 – 4x + 4
Answers
Answer: x = -2, \(\frac{2 }{3}\)
Step-by-step explanation:
Given:
0 = –3x² – 4x + 4
The quadratic formula:
\(\displaystyle x=\frac{-b\pm\sqrt{b^2-4ac} }{2a}\)
Substitute known values:
* a = -3, b = -4, c = 4
\(\displaystyle x=\frac{-(-4)\pm\sqrt{(-4)^2-4(-3)(4)} }{2(-3)}\)
Simplify with multiplication:
\(\displaystyle x=\frac{4\pm\sqrt{16+48} }{-6}\)
Simplify:
\(\displaystyle x=\frac{4\pm\sqrt{64} }{-6}\)
\(\displaystyle x=\frac{4+8 }{-6}\), \(\displaystyle x=\frac{4-8 }{-6}\)
\(\displaystyle x=\frac{12 }{-6}\), \(\displaystyle x=\frac{-4 }{-6}\)
FOR 100 POINTS!!!!!!!!!!!
A food truck did a daily survey of customers to find their food preferences. The data is partially entered in the frequency table. Complete the table to analyze the data and answer the questions:
Likes hamburgers Does not like hamburgers Total
Likes burritos 29 41
Does not like burritos 54 135
Total 110 205
Part A: What percentage of the survey respondents liked neither hamburgers nor burritos? Show all work. (3 points)
Part B: What is the marginal relative frequency of all customers who like hamburgers? Show all work. (3 points)
Part C: Is there an association between liking burritos and liking hamburgers? Use ratios of joint and marginal frequencies to support your answer. (4 points)
Answers
Answer:
Part A:
To find the percentage of survey respondents who liked neither hamburgers nor burritos, we need to calculate the frequency in the "Does not like hamburgers" and "Does not like burritos" categories.
Frequency of "Does not like hamburgers" = Total in "Does not like hamburgers" category = 135
Frequency of "Does not like burritos" = Total in "Does not like burritos" category = 54
Total respondents who liked neither hamburgers nor burritos = Frequency of "Does not like hamburgers" + Frequency of "Does not like burritos" = 135 + 54 = 189
Percentage of survey respondents who liked neither hamburgers nor burritos = (Total respondents who liked neither hamburgers nor burritos / Total respondents) x 100
Percentage = (189 / 205) x 100 = 92.2%
Therefore, 92.2% of the survey respondents liked neither hamburgers nor burritos.
Part B:
To find the marginal relative frequency of all customers who like hamburgers, we need to divide the frequency of "Likes hamburgers" by the total number of respondents.
Frequency of "Likes hamburgers" = 110 (given)
Total respondents = 205 (given)
Marginal relative frequency = Frequency of "Likes hamburgers" / Total respondents
Marginal relative frequency = 110 / 205 ≈ 0.5366 or 53.66%
Therefore, the marginal relative frequency of all customers who like hamburgers is approximately 53.66%.
Part C:
To determine if there is an association between liking burritos and liking hamburgers, we can compare the joint and marginal frequencies.
Joint frequency of "Likes hamburgers" and "Likes burritos" = 29 (given)
Marginal frequency of "Likes hamburgers" = 110 (given)
Marginal frequency of "Likes burritos" = 70 (calculated by adding the frequency of "Likes burritos" in the table)
To assess the association, we compare the ratio of the joint frequency to the product of the marginal frequencies:
Ratio = Joint frequency / (Marginal frequency of "Likes hamburgers" x Marginal frequency of "Likes burritos")
Ratio = 29 / (110 x 70)
Ratio ≈ 0.037 (rounded to three decimal places)
Find the missing length for the pair of similar figures.

Answers
Answer:
a = 4.5
Step-by-step explanation:
In easy way you can understand by this simple way
if 4m half is 2m
so, 9m half is 4.5
in simple way answer
a boy was 28 inches tall. Currently, he is 25% taller. How
tall is the boy now?
Answers
Answer:
21 inches
Step-by-step explanation:
If the boy is 25% smaller, that means his current height is 75% of his previous height. 75% of 28 is 0.75 * 28 which is 21.
Hope this helps :)
Answer:
35 inches tall. (This is assuming they want him to be 25% taller. Using the past tense of 28, I assume this is growth.)
Step-by-step explanation:
25% is 25/100 therefore we get 1/4 which gives us 28/4 = 7.
So this makes the boy 7 inches taller than 28.
28 + 7 = 35
Making him 35 inches tall.
9. If the perimeter of an isosceles triangle is 83 cm. and its base is 23 cm. Find the measure of its equal sides.
10. The perimeter of a rhombus is 5.6 cm. Find its side.
11. The perimeter of a rectangle is equal to that of a square with side 17 m. If the length of the
rectangle is 26 m. What is its breadth ?
12. What is the cost of fencing a rectangular field of length 16 m and breadth 11 m at the rate of 12 per m.
Please solve all questions..step by step.
Answers
9.
Q:-If the perimeter of an isosceles triangle is 83 cm. and its base is 23 cm. Find the measure of its equal sides.
Answer:- As we know that Perimeter is the sum of all sides.
Let the both side be x83 = 23 + (x + x)83 - 23 = 2x60 = 2x30 = xOther two sides are 30 cm.
10.The perimeter of a rhombus is 5.6 cm. Find its side.
Answer:- As we know that
Side of Rhombus = Perimeter/4
Side = 5.6/4Side = 1.4 cmSide is 1.4 cm11.The perimeter of a rectangle is equal to that of a square with side 17 m. If the length of the
The perimeter of a rectangle is equal to that of a square with side 17 m. If the length of therectangle is 26 m. What is its breadth ?
Answer:- Perimeter of square = 4 × s
Perimeter = 4 × 17Perimeter = 68 cmNow,
Perimeter of rectangle = 2(l + b)68 = 2(26 + b)68/2 = 26 + b34 = 26 + b34 - 26 = b8 = bb=812.What is the cost of fencing a rectangular field of length 16 m and breadth 11 m at the rate of 12 per m.
Answer:- Perimeter = 2(l + b)
Perimeter = 2(16 + 11)Perimeter = 2(27)Perimeter = 54 cmNow,
Total cost = 54 × 12Total cost = ₹648.\(\begin{gathered} \\ \end{gathered}\)
Joseph has a bag filled with 2 red, 4 green, 10 yellow, and 9 purple marbles. Determine P(not purple) when choosing one marble from the bag.
64%
36%
24%
8%
(no links)
Answers
The probability P(not purple) is (a) 64%
How to determine the probability P(not purple)From the question, we have the following parameters that can be used in our computation:
2 red, 4 green, 10 yellow, and 9 purple marbles.
This means that
P(not purple) = (not purple)/Total
Substitute the known values in the above equation, so, we have the following representation
P(not purple) = (2 + 4 + 10)/(2 + 4 + 10 + 9)
Evaluate
P(not purple) = 64%
Hence, the probability is 64%
Read more about probability at
https://brainly.com/question/251701
#SPJ1
Kevin drew square WXYZ on this grid. Kevin translated the square 3 units along the x- axis and -1 unit along the y -axis. What are the new coordinates of the square?
Answers
By dilation the square's new coordinates are W'(3, 2), X'(3, 4), Y'(1, 4), and Z' (1, 2).
DILATION: WHAT IS IT?Dilation is a transition in geometry that alters an object's size without altering its general shape. Given that it is a non-rigid transformation, the preimage and image are not congruent, and the distance between their points does not stay constant. Dilation can describe either a growth or a contraction in size1.
For instance, if we enlarge a square by a factor of 2, its area will increase by four times and each of its sides will be twice as long as before. A circle will have a radius that is three-fourths longer than previously and an area that is nine-sixteenths larger if we dilate it by a factor of 3/4.
In geometry, translation is a rigid transformation that maintains the size and shape of a figure while shifting each point by the same amount in a certain direction.
. To translate a square, we shift each corner to its new location by the specified distance.
Kevin translated the square in this instance by 3 units along the x-axis and -1 unit along the y-axis
. So, to obtain the new coordinates of the square W'X'Y'Z', we add 3 to each x-coordinate and remove 1 from each y-coordinate of the original square WXYZ.
- W'(3, 2) (3, 2)
- X'(3, 4) (3, 4)
- Y'(1, 4) (1, 4)
- Z'(1, 2) (1, 2)
To know more about dilation visit:
brainly.com/question/13176891
#SPJ9
What is the solution to - 2 (4p + 12) = 8(p - 11)?
Answers
I need help please help me

Answers
Answer:
For part D, x=5.217
Step-by-step explanation:
So essentially, all triangles have 180 degrees, so we an set up our equation as
55 + 8x + 15x + 5 = 180. We can simplify it to 60 + 23x = 180 by combining the like terms. Then we subtract 60 from both sides, getting us 23x = 120, and then we just divide 23 from both sides, and I just rounded the number to the thousandth place.
For part B, we an apply that same logic, and add 38 + 38 + 4x +... = 180. This gives us 76 + 4x+ ... = 180, and from there we just apply basic algebra. Hope this helps and lmk if you have and questions :D
Whats the slope of (-3,4) (0, 0)
Answers
Answer:
slope = \(-\frac{4}{3}\)
Step-by-step explanation:
Use the slope formula, \(m = \frac{y_2-y_1}{x_2-x_1}\), to find the slope. \(m\) represents the slope. \(x_1\) and \(y_1\) represent the x and y values of one point, and \(x_2\) and \(y_2\) represent the x and y values of another point. So, substitute the x and y values of the points (-3, 4) and (0, 0) into the formula appropriately and solve:
\(m= \frac{(0)-(4)}{(0)-(-3)} \\m = \frac{0-4}{0+3} \\m = \frac{-4}{3}\)
Thus, the slope is \(-\frac{4}{3}\).
The graph below shows a line of best fit for data collected on the distance drivers traveled as a function of time. Which of the following is the equation of the line of best fit? A. B. C. D.
Answers
The equation for the line of best fit is given as follows:
y = 50x/3.
How to define a linear function?The slope-intercept equation for a linear function is presented as follows:
y = mx + b.
The parameters of the definition of the linear function are given as follows:
m represents the slope of the function, which is by how much the dependent variable y increases(positive) or decreases(negative) when the independent variable x is added by one.b represents the y-intercept of the function, representing the numeric value of the function when the input variable x has a value of 0. On the case of the graph, the intercept is given by the value of y at which the graph crosses or touches the y-axis.From the graph, when x = 0, y = 0, hence the intercept b is given as follows:
b = 0.
Hence:
y = mx.
When x = 3, y = 50, hence the slope m is given as follows:
3m = 50
m = 50/3.
Hence the equation is:
y = 50x/3.
More can be learned about linear functions at https://brainly.com/question/15602982
#SPJ1
