a basket contains 9 blue ribbons, 7 red ribbons, and 6 white ribbons. what is the probability that three ribbons selected at random will be red?
Answers
The probability of selecting three red ribbons at random from the basket is approximately 2.27%.
In order to calculate the probability of selecting three red ribbons from a basket containing 9 blue, 7 red, and 6 white ribbons, we need to use the concept of combinations.
A combination represents the number of ways to choose items from a larger set without considering the order.
First, let's determine the total number of ways to choose 3 ribbons from the 22 ribbons in the basket (9 blue + 7 red + 6 white). This can be calculated using the combination formula: C(n, k) = n! / (k!(n-k)!), where n is the total number of items and k is the number of items to choose. In this case, n = 22 and k = 3. So, C(22, 3) = 22! / (3!(22-3)!) = 22! / (3!19!) = 1540 possible combinations.
Now, let's find the number of ways to choose 3 red ribbons from the 7 red ribbons available. Using the combination formula again, C(7, 3) = 7! / (3!(7-3)!) = 7! / (3!4!) = 35 combinations.
Finally, to calculate the probability of choosing three red ribbons, we'll divide the number of ways to choose 3 red ribbons by the total number of ways to choose any 3 ribbons: Probability = 35/1540 ≈ 0.0227, or approximately 2.27%.
To learn more about probability click here
brainly.com/question/30034780
#SPJ11
Related Questions
A person swims 6.4 meters per
second north while being
pushed by a current moving
west at 2.1 meters per second.
What is the magnitude of the
swimmer's resultant vector?
Answers
Answer:
4.3
im not sure
correct me if im wrong
Answer
6.7
Step-by-step explanation:
Works on acellus
Find the ratio a:c if
a:b = 1:2, b:d = 4:5, d:c = 3:1
Answers
Answer:
a : c = 6 : 5
Step-by-step explanation:
Expressing the ratios in fractional form, then
\(\frac{a}{c}\) = \(\frac{a}{b}\) × \(\frac{b}{d}\) × \(\frac{d}{c}\) = \(\frac{1}{2}\) × \(\frac{4}{5}\) × \(\frac{3}{1}\) = \(\frac{12}{10}\) = \(\frac{6}{5}\)
Thus a : c = 6 : 5
Based on the graph, what does the point (2, 60) represent?
A.
The plant grew 60 cm in 2 days.
B.
The plant grew 30 cm in 2 months.
C.
The plant grew 2

Answers
Answer:
The plant grew 60 cm in 2 months.
Step-by-step explanation:
The point is at 2,60
Please help me Write the phrase as an expression.
13 subtracted from a number x
An expression is =?

Answers
Answer:
a. The equation is 33+m
b. 333 dollars
Step-by-step explanation:
The phrase can be written as a mathematical expression in the form x - 13
Subtract means minus( - )
let
x = unknown number
An unknown number is a value which is not know and can be determined by solving an equation13 subtracted from a number x
x - 13 is the mathematical expression
Therefore, the phrase "13 subtracted from a number x" can be written as x - 13
Read more:
https://brainly.com/question/19952256
Compare and Contrast: Two equations are listed below. Solve each equation and compare the solutions. Choose the statement that is true
about both solutions. (2 points)
Equation 1 Equation 2
5x - 61 = -41 17x + 131 = 27
оа
Equation 1 has more solutions than equation 2.
Ob
Equation 1 and Equation 2 have the same number of solutions.
ос
Equation 2 has more solutions than Equation 1.
Od
The number of solutions cannot be determined.
Answers
Answer:
equation 2
Step-by-step explanation:
Find lateral surface area in square units, of the following 3-
dimensional figure.
Enter just a number for your answer.
-
14 ft
7 ft
9 ft

Answers
Answer:
Lateral surface area of cuboid = 448 ft²
Step-by-step explanation:
Given:
Height of cuboid(h) = 14 ft
Length of cuboid(l) = 9 ft
width of cuboid(b) = 7 ft
Find:
Lateral surface area of cuboid
Computation:
Lateral surface area of cuboid = 2 h(l + b)
Lateral surface area of cuboid = 2(14)(9 + 7)
Lateral surface area of cuboid = 28(16)
Lateral surface area of cuboid = 448 ft²
1. Evaluate f(x) = -4x - 7 for x = -2.
Answers
Answer:
1
Step-by-step explanation:
Not sure how to answer it but here's the correct answer i believe
If x=3yz^2, what is y in terms of x and z?
Answers
Two or more expressions with an Equal sign is called as Equation. y=x/3z^2 for equation x=3yz^2 in terms of x and z
What is Equation?Two or more expressions with an Equal sign is called as Equation.
The given equation is x equal to three y z square.
x=3yz²
We need to solve for y.
We need to separate y from other variables.
Divide both sides by 3z²
x/3z²=y
Hence y=x/3z² for equation x=3yz² in terms of x and z
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
The Lewiston Company issues 23-year bonds, but it pays nocoupon. Calculate the price per $1,000 face value of thiszero-coupon bond using an interest rate of 6.7%. Answer to thenearest cent.
Answers
The price per $1,000 face value of the zero-coupon bond issued by the Lewiston Company is approximately $288.12.
To calculate the price of the zero-coupon bond, we can use the present value formula:
Price = Face Value / (1 + Interest Rate)^(Number of Years)
In this case, the face value is $1,000, the interest rate is 6.7%, and the number of years is 23.
Price = 1000 / (1 + 0.067)^23 = 1000 / 2.871 = $348.35
However, this value represents the future value of the bond. To determine the present value, we need to discount it to today's value. To do that, we can divide the future value by (1 + Interest Rate).
Present Value = Price / (1 + Interest Rate) = 348.35 / (1 + 0.067) = $288.12 (rounded to the nearest cent)
The price per $1,000 face value of the zero-coupon bond issued by the Lewiston Company, using an interest rate of 6.7%, is approximately $288.12. Zero-coupon bonds are sold at a discount to their face value because they do not pay any periodic interest payments. The price reflects the present value of the bond, taking into account the time value of money and the specified interest rate.
To know more about bond follow the link:
https://brainly.com/question/29282058
#SPJ11
Chebyshev's theorem provides the proportion of observations that lie within k standard deviations of the mean. The value k must be ______.
Answers
The value of k in Chebyshev's theorem can be any positive real number.
Chebyshev's theorem, also known as Chebyshev's inequality, is a statistical theorem that provides an upper bound on the proportion of observations that lie within a certain number of standard deviations from the mean in any distribution.
The theorem states that for any distribution (regardless of its shape), at least \((1 - 1/k^2)\) proportion of the data falls within k standard deviations from the mean, where k is any positive number greater than 1.
Mathematically, Chebyshev's theorem can be expressed as:
P(|X - μ| < kσ) ≥ \(1 - 1/k^2\)
Where:
P(|X - μ| < kσ) represents the probability that a randomly selected observation from the distribution falls within k standard deviations from the mean.
μ represents the mean of the distribution.
σ represents the standard deviation of the distribution.
k is the number of standard deviations from the mean.
The value of k in Chebyshev's theorem can be any positive real number.
Learn more about Chebyshev's theorem at:
brainly.com/question/231802
#SPJ4
At time t, a particle moving in the xy-plane is at position (x(t), y(t)), where x(t) and y(t) are not explicitly given. For t≥0, dx/dt=4t+1 and dy/dt=sin(t^2). At time t=0, x(0)=0 and y(0)=-4. a) Find the speed of the particle at time t=3, and find the acceleration vector of the particle at time t=3. b) Find the slope of the line tangent to the path of the particle at time t=3. c) Find the position of the particle at time t=3. d) Find the total distance traveled by the particle over the time interval 0≤t≤3.
Answers
The speed of the particle at t=3 is approximately 13.002and the acceleration vector at t=3 is approximately <4, 6cos(9)>. The slope of the tangent line at t=3 is approximately -0.249. The position of the particle at t=3 is approximately (21, -3.987). The total distance travelled by the particle over the time interval 0≤t≤3 is approximately 7.656 units
To find the speed of the particle at time t=3, we need to find the magnitude of the velocity vector at t=3. Using the given information, we have:
dx/dt = 4t+1, so at t=3, dx/dt = 13
dy/dt = sin(t^2), so at t=3, dy/dt = sin(9)
Therefore, the velocity vector at t=3 is v(3) = (13, sin(9)). The speed of the particle at t=3 is the magnitude of this vector:
||v(3)|| = sqrt(13^2 + sin(9)^2) ≈ 13.002
To find the acceleration vector of the particle at t=3, we need to find the derivatives of dx/dt and dy/dt with respect to t:
d^2x/dt^2 = 4
d^2y/dt^2 = 2t*cos(t^2)
Plugging in t=3, we get:
d^2x/dt^2 = 4
d^2y/dt^2 = 6cos(9)
Therefore, the acceleration vector at t=3 is a(3) = (4, 6cos(9)).
The slope of the line tangent to the path of the particle at time t=3 is the same as the slope of the velocity vector at t=3. The velocity vector at t=3 is v(3) = (13, sin(9)), so its slope is:
slope = (change in y) / (change in x) = sin(9) / 13 = -0.249 ( approx)
To find the position of the particle at time t=3, we need to integrate the velocity vector from t=0 to t=3 and add the initial position. Using the given initial conditions, we have:
x(0) = 0, y(0) = -4
Integrating dx/dt = 4t+1, we get:
x(t) = 2t^2 + t + C
Using x(0) = 0, we get C = 0, so x(t) = 2t^2 + t.
Integrating dy/dt = sin(t^2), we get:
y(t) = -cos(t^2) + C
Using y(0) = -4, we get C = -3, so y(t) = -cos(t^2) - 3.
Therefore, the position of particle at time t=3 is:
(2(3)^2 + 3, -cos(9) - 3) ≈ (21, -3.987)
To find the total distance traveled by the particle over the time interval 0≤t≤3, we need to integrate the speed (magnitude of the velocity vector) over this interval. Using the expression for ||v(t)|| from part (a), we have:
distance = ∫[0,3] ||v(t)|| dt
= ∫[0,3] sqrt((4t+1)^2 + sin(t^2)^2) dt
This integral cannot be evaluated analytically, so we will approximate it using numerical integration. One way to do this is to use Simpson's rule with a step size of 0.1 (n=30):
distance ≈ 7.656
Therefore, the total distance traveled by the particle over the time interval 0≤t≤3 is approximately 7.656 units.
To know more about Distance travelled;
https://brainly.com/question/29338141
#SPJ4
Simplify the following expression

Answers
pls help
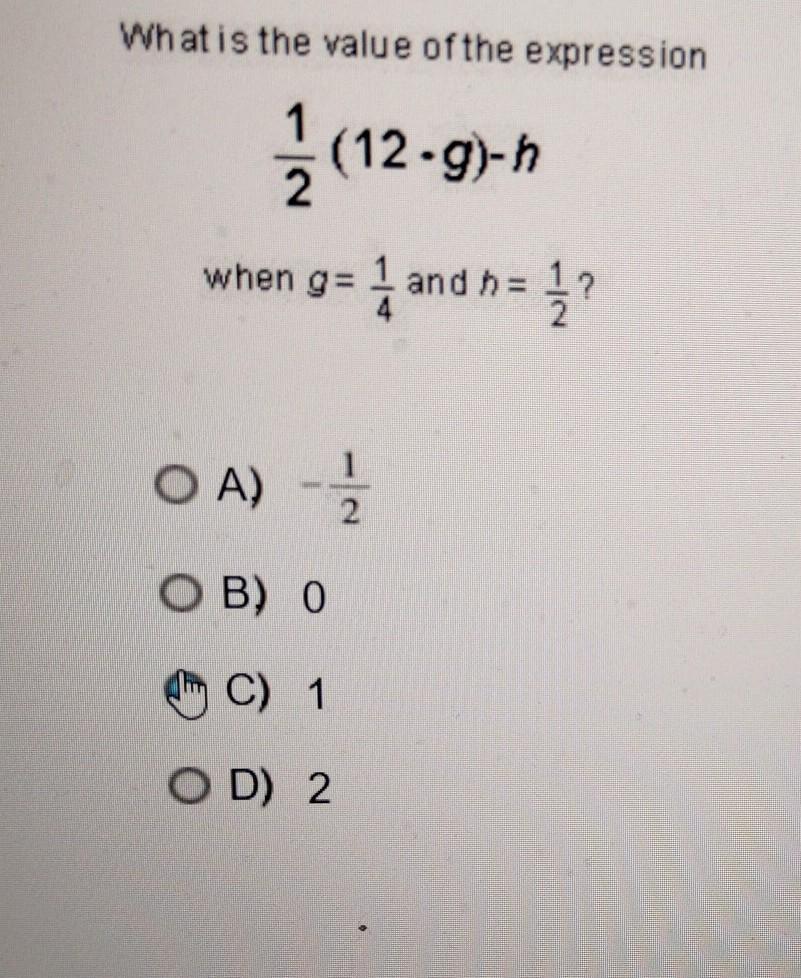
Answers
Answer:
c) 1
Step-by-step explanation:
\(\frac{1}{2}\)(12·g)-h
g= \(\frac{1}{4}\) and h=\(\frac{1}{2}\); substitute back in the equation
\(\frac{1}{2}\)(12·\(\frac{1}{4}\)) - \(\frac{1}{2}\); multiply inside the parenthesis
\(\frac{1}{2}\)(3)- \(\frac{1}{2}\); multiply and notice the same denominator
\(\frac{3}{2}\)-\(\frac{1}{2}\) = \(\frac{2}{2}\) = 1; subtract the fractions
How to find the dimensions of the hoses in hydraulics (for
advance and return).
force of advance = 293 KN
force of return = 118KN
Answers
The diameter of the hose for return is approximately 22.7 mm.
In hydraulics, hoses are a crucial part of the system as they transfer the hydraulic fluid that transmits power to the actuators. In order to select the right hoses, it is important to consider factors such as the flow rate, pressure drop, and the length of the hoses.
Q = (A x V)/60
Where:
Q = flow rate in liters per minute (lpm)
A = area of the hose in square millimeters (mm²)
V = velocity of the fluid in meters per second (m/s)
60 = conversion factor from seconds to minutes
The force of advance and return can be used to determine the pressure of the system. We can then use the pressure drop and the length of the hoses to find the flow rate. Finally, we can use the flow rate to find the area of the hoses.
For the force of advance:
Pressure = force/area
Area = force/pressure
Assuming a pressure drop of 5 bar and a hose length of 10 meters, we can find the flow rate as follows:
Flow rate = (1000 x 293)/((5 x 10) + 1000)
Flow rate = 54.98 lpm
Using the formula Q = (A x V)/60, we can find the area of the hose as follows:
A = (Q x 60)/V
Assuming a fluid velocity of 4 m/s, we get:
A = (54.98 x 60)/(4 x π x (0.0127/2)²)
A = 1005.2 mm²
Therefore, the diameter of the hose for advance is approximately 36.0 mm.
For the force of return:
Pressure = force/area
Area = force/pressure
Assuming a pressure drop of 5 bar and a hose length of 10 meters, we can find the flow rate as follows:
Flow rate = (1000 x 118)/((5 x 10) + 1000)
Flow rate = 22.11 lpm
Using the formula Q = (A x V)/60, we can find the area of the hose as follows:
A = (Q x 60)/V
Assuming a fluid velocity of 4 m/s, we get:
A = (22.11 x 60)/(4 x π x (0.0127/2)²)
A = 404.1 mm²
Therefore, the diameter of the hose for return is approximately 22.7 mm.
To know more about diameter, visit:
https://brainly.com/question/32968193
#SPJ11
Can anyone solve this question please
The ordered pair (1,7)belongs to some function,f(x). Explain why the ordered pair(8,1) cannot belong to the inverse of this function.
Answers
Answer:
Step-by-step explanation:
by definition : The inverse of a relation consisting of points of the form (x,y) is the set of points (y,x)
if (1,7) is a point belong to f(x), then the inverse has to be (7,1) not (8,1)
Ordered pair\((8, 1)\) cannot belong to the inverse of the given function because ordered pair \((7,1).\)belong to the inverse function of the given function.
What is inverse function?
" Inverse function is defined as when the domain and range of a function interchange with each other of the given function. It is represented by\(y = g(x)\)then its inverse is \(x = f(y)\)"
According to the question,
Given function,
Function\(f(x)\) with ordered pair \((1,7)\)
Domain of a function\(= 1\)
Range of a function \(= 7\)
As per the definition of inverse function,
Domain of inverse function \(= 7\)
Range of a inverse function \(= 1\)
Ordered pair\((7, 1)\) belongs to inverse of the given function.
Hence, ordered pair\((8, 1)\) cannot belong to the inverse of the given function.
Learn more about inverse function here
https://brainly.com/question/2541698
#SPJ2
The angles shown are supplementary. What is the value of x ?

Answers
Answer:
D
Step-by-step explanation:
This is because if u subsitute x with 17, 17x5 is 85 and 85+95= 180
\(\color{plum}\tt\bold{(D) \: 17}\)
○=> Steps to derive correct answer :Given :
▪︎Angle (5x)° and angle 95° are supplementary angles.
Which means :
\( = \tt5x + 95 = 180\)
\( = \tt5x = 180 - 95\)
\( = \tt5x = 85\)
\( \hookrightarrow\tt \color{plum}x = 17\)
Thus, the value of x = 17
Let us check whether or not we have found out the correct value of x by placing 17 in the place of x:
\( =\tt5 \times 17 + 95 = 180\)
\( =\tt 85 + 95 = 180\)
\( =\tt 180 = 180\)
Since the sum of both angles is equivalent to 180[85+95=180], we can conclude that we have found out the correct value of x.
Therefore, the correct option is (D) 17
A school band is buying new jackets and hats. A jacket
costs $100 and a hat costs $40. The expression 100j + 40h
represents the cost of į jackets and h hats. How much will 5
new jackets and 8 new hats cost?
Answers
Answer:
it will cost 1820
Step-by-step explanation:
add 100 + 40=140 x 13=1820
Hoped it helps
Number of Students
10
8
6
4
2
0
Test Scores for Ms. Gioia's Science Class
71-75 76-80 81-85 86-90 91-95 96-100
Science Test Scores
2) How many students in Ms. Gioia's class took the science test?
Answers
In the histogram , the number of students in Ms. Gioia's class took the science test is 27.
What is histogram?
A grouped frequency distribution with continuous classes is graphically represented by a histogram. It is an area diagram, and its size is proportional to the frequencies in the associated classes. Due to the base's coverage of the spaces between class boundaries, all of the rectangles in such representations are contiguous.
Here according to the histogram ,
The number of students score between 71-75 = 4
The number of students score between 76-80 = 6
The number of students score between 86-90 =8
The number of students score between 91-95 = 7
The number of student score between 96-100 = 2
Then number of students in Ms. Gioia's class took the science test is,
=> 4+6+8+7+2 = 27
Hence the number of students in Ms. Gioia's class took the science test is 27.
To learn more about histogram refer the below link
https://brainly.com/question/2962546
#SPJ9
2x + y = 7 3x -2y = -7 solve by substitution
Answers
Answer:
Solve for the first variable in one of the equations, then substitute the result into the other equation.
Point Form:
(1, 5)
Equation Form:
x = 1, y = 5
Brainliest Please!!

The solution for the given equations: x = 1 , y = 5.
What is substitution method?The substitution method is the algebraic method to solve simultaneous linear equations. As the word says, in this method, the value of one variable from one equation is substituted in the other equation.
Given, equations
2x + y = 7 -------(a)
3x -2y = -7 -------(b)
Taking equation (a)
2x + y =7
y = 7 - 2x ------(c)
Substituting value of y in equation (b) from equation (c)
3x - 2(7 - 2x) = -7
3x - 14 + 4x = -7
7x = 7
x = 1
Putting value of x in equation (c)
y = 7 - 2 (1)
y = 5
Hence, x = 1 and y = 5 is the solution for the given equations 2x + y = 7 and 3x -2y = -7.
Learn more about substitution method here:
https://brainly.com/question/14619835
#SPJ2
The leftmost digits of two multi-digit numbers are 3 and 6. Can you tell
which number is greater? Explain.
Answers
Answer:
You cannot tell which number is greater, we need more information.
"multi-digit" does not imply how many digits each number has, therefore both numbers could be greater, for example:
3005 vs 60
OR
30 vs 645
A + B + C = 12
4A - 4B + 2C = -16 -
3A + 3B - C = 4
Solve the system
Answers
Answer:
Step-by-step explanation:
Add them all together which is
ABC124A4B2C-16-3A3B-C yep
use the definition of the definite integral (with right endpoints) to evaluate ∫ (4 − 2)
Answers
The value of the definite integral \(\(\int_2^5 (4-2x) dx\)\) is 6.
To evaluate the integral \(\(\int_2^5 (4-2x) dx\)\) using the definition of the definite integral with right endpoints, we can partition the interval \(\([2, 5]\)\) into subintervals and approximate the area under the curve \(\(4-2x\)\) using the right endpoints of these subintervals.
Let's choose a partition of \(\(n\)\) subintervals. The width of each subinterval will be \(\(\Delta x = \frac{5-2}{n}\)\).
The right endpoints of the subintervals will be \(\(x_i = 2 + i \Delta x\)\), where \(\(i = 1, 2, \ldots, n\)\).
Now, we can approximate the integral as the sum of the areas of rectangles with base \(\(\Delta x\)\) and height \(\(4-2x_i\)\):
\(\[\int_2^5 (4-2x) dx \approx \sum_{i=1}^{n} (4-2x_i) \Delta x\]\)
Substituting the expressions for \(\(x_i\)\) and \(\(\Delta x\)\), we have:
\(\[\int_2^5 (4-2x) dx \approx \sum_{i=1}^{n} \left(4-2\left(2 + i \frac{5-2}{n}\right)\right) \frac{5-2}{n}\]\)
Simplifying, we get:
\(\[\int_2^5 (4-2x) dx \approx \sum_{i=1}^{n} \frac{6}{n} = \frac{6}{n} \sum_{i=1}^{n} 1 = \frac{6}{n} \cdot n = 6\]\)
Taking the limit as \(\(n\)\) approaches infinity, we find:
\(\[\int_2^5 (4-2x) dx = 6\]\)
Therefore, the value of the definite integral \(\(\int_2^5 (4-2x) dx\)\) is 6.
The complete question must be:
3. Use the definition of the definite integral (with right endpoints) to evaluate \($\int_2^5(4-2 x) d x$\)
Learn more about integral :
https://brainly.com/question/18125359
#SPJ11
Which is similar to triangle PQR?

Answers
The answer choice which represents a triangle which is similar to PQR is; Choice D.
Which Triangle is similar to the given triangle PQR?As evident in the task content; the answer choice which represents a triangle simar to triangle PQR is to be determined.
On this note, by determining the ratio of the sides given; 21 / 18 = 7 / 6.
On this note, the answer choice which represents a triangle which is similar to triangle PQR is the triangle in which the ratio is sides is same.
Hence, in Choice D; 17.5 / 15 = 7 / 6. Ultimately, the similar triangle is choice D.
Read more on similar triangles;
https://brainly.com/question/14285697
#SPJ1
In Problems 23–34, find the integrating factor, the general solu- tion, and the particular solution satisfying the given initial condition. 24. y' – 3y = 3; y(0) = -1
Answers
The particular solution is:
y = -1 - e^(3x)
We have the differential equation:
y' - 3y = 3
To find the integrating factor, we multiply both sides by e^(-3x):
e^(-3x)y' - 3e^(-3x)y = 3e^(-3x)
Notice that the left-hand side is the product rule of (e^(-3x)y), so we can write:
d/dx (e^(-3x)y) = 3e^(-3x)
Integrating both sides with respect to x, we get:
e^(-3x)y = ∫ 3e^(-3x) dx + C
e^(-3x)y = -e^(-3x) + C
y = -1 + Ce^(3x)
Using the initial condition y(0) = -1, we can find the value of C:
-1 = -1 + Ce^(3*0)
C = -1
So the particular solution is:
y = -1 - e^(3x)
To know more about integrating factor refer here:
https://brainly.com/question/25527442
#SPJ11
Solve each inequality. p + 5 < 10 A. p < –15 B. p < 5 C. p < 15 D. p < –5
Answers
Answer:
B) p<5
Step-by-step explanation:
Let $f$ be a function such that $f(x+y) = x + f(y)$ for any two real numbers $x$ and $y$.
If $f(0) = 2$, then what is $f(2021)?$
Answers
Given:
f(0) = 2
So first of all, we let x = 2021, y = 0:
Then, F(2021) = 2021 + f(0)
Since f(0) = 2, then f(2021) = 2021 + 2 = 2023.
To add, the process that relates an input to an output is called a function.
There are always three main parts of a function, namely:
Input
The Relationship
The Output
The classic way of writing a function is "f(x) = ... ".
What goes into the function is put inside parentheses () after the name of the function: So, f(x) shows us the function is called "f", and "x" goes in.
What a function does with the input can be usually seen as:
f(x) = x2 reveals to us that function "f" takes "x" and squares it.
Consider the PDE au(x, t) = 4 d²u(x, t) 2 Ət əx² For each of BCs and ICs, solve the initial value problem. du(π,t) a) BCs: u(0,t)=0 = = 0 and əx IC: u(x,0) = x ANSWER: f(x)= n=1 u(2,t) = 0 and u(0,t)=0 u(x,0)=sin x ANSWER: f(x)=¹1_sin(2 + nx) na n=1 1+ 2 X b) BCs: IC: 8 (2n-1) T n+1 (-1)041 -4(2n-1)²t sin(2-nπ) nπ 1- 2 e sin (2n-1) 2 na sin X 2 -(nn)²t x -X
Answers
the solution for the initial value problem is: u(x, t) = sin(sqrt(-λ² * (a / 4)) * x) * exp(-λ² * t) where λ = ± sqrt(-4n² / a), and n is a non-zero integer.
The given partial differential equation is:
au(x, t) = 4 * (d²u(x, t) / dt²) / (dx²)
a) BCs (Boundary Conditions):
We have u(0, t) = 0 and u(π, t) = 0.
IC (Initial Condition):
We have u(x, 0) = x.
To solve this initial value problem, we need to find a function f(x) that satisfies the given boundary conditions and initial condition.
The solution for f(x) can be found using the method of separation of variables. Assuming u(x, t) = X(x) * T(t), we can rewrite the equation as:
X(x) * T'(t) = 4 * X''(x) * T(t) / a
Dividing both sides by X(x) * T(t) gives:
T'(t) / T(t) = 4 * X''(x) / (a * X(x))
Since the left side only depends on t and the right side only depends on x, both sides must be equal to a constant value, which we'll call -λ².
T'(t) / T(t) = -λ²
X''(x) / X(x) = -λ² * (a / 4)
Solving the first equation gives T(t) = C1 * exp(-λ² * t), where C1 is a constant.
Solving the second equation gives X(x) = C2 * sin(sqrt(-λ² * (a / 4)) * x) + C3 * cos(sqrt(-λ² * (a / 4)) * x), where C2 and C3 are constants.
Now, applying the boundary conditions:
1) u(0, t) = 0:
Plugging in x = 0 into the solution X(x) gives C3 * cos(0) = 0, which implies C3 = 0.
2) u(π, t) = 0:
Plugging in x = π into the solution X(x) gives C2 * sin(sqrt(-λ² * (a / 4)) * π) = 0. To satisfy this condition, we need the sine term to be zero, which means sqrt(-λ² * (a / 4)) * π = n * π, where n is an integer. Solving for λ, we get λ = ± sqrt(-4n² / a), where n is a non-zero integer.
Now, let's find the expression for u(x, t) using the initial condition:
u(x, 0) = X(x) * T(0) = x
Plugging in t = 0 and X(x) = C2 * sin(sqrt(-λ² * (a / 4)) * x) into the equation above, we get:
C2 * sin(sqrt(-λ² * (a / 4)) * x) * C1 = x
This implies C2 * C1 = 1, so we can choose C1 = 1 and C2 = 1.
Therefore, the solution for the initial value problem is:
u(x, t) = sin(sqrt(-λ² * (a / 4)) * x) * exp(-λ² * t)
where λ = ± sqrt(-4n² / a), and n is a non-zero integer.
Note: Please double-check the provided equation and ensure the values of a and the given boundary conditions are correctly represented in the equation.
To know more about Equation related question visit:
https://brainly.com/question/29657983
#SPJ11
kiki has a piece of string that she cuts into smaller pieces. this line plot shows the lengths of the pieces. raj has a piece of string that is 12 as long as kiki's third-longest piece. (note: the problem says third-longest piece, not third-longest length.) how long is raj's piece of string? enter your answer as a mixed number in simplest form by filling in the boxes.
Answers
The length of Raj's piece of string is 12x units.
What is the area of a triangle with base length 8 units and height 5 units?To determine the length of Raj's piece of string, we need to find Kiki's third-longest piece.
Looking at the line plot or list of lengths provided, we can identify the third-longest length of Kiki's pieces.
Let's assume Kiki's third-longest piece has a length of x units.
According to the problem, Raj's piece of string is 12 times as long as Kiki's third-longest piece.
Therefore, the length of Raj's piece of string would be 12 × x units.
We can only express it as 12x units, where x represents the length of Kiki's third-longest piece.
Learn more about triangle
brainly.com/question/2773823
#SPJ11
Solve each inequality. Check your solution. (x/3) + 5 ≥ 1/6
Answers
The inequality given by (x/3) + 5 ≥ 1/6 has the solution x ≥ -29/2 or [-29/2 , +∞).
Inequality refers to the relationship between two non-equal expressions. It can be denoted by > for greater than, < for less than, >/= for greater than and equal to, and </= for less than and equal to.
To solve an inequality is to find the values of x such that when we substitute that number for x we have a true statement.
Given the inequality (x/3) + 5 ≥ 1/6, subtract 5 from both sides.
(x/3) + 5 - 5 ≥ 1/6 - 5
x/3 ≥ -29/6
Multiply both sides by 3.
3(x/3) ≥ 3(-29/6)
x ≥ -29/2
To check, let x = -29/2
x = -29/2 ≥ -29/2
Substitute this value to the inequality.
(x/3) + 5 ≥ 1/6
(-29/2)/3 + 5 ≥ 1/6
1/6 ≥ 1/6
let x = -14,
x = -14 ≥ -29/2
Substitute this value to the inequality.
(x/3) + 5 ≥ 1/6
-14/3 + 5 ≥ 1/6
1/3 ≥ 1/6
Learn more about inequalities here: brainly.com/question/24372553
#SPJ4
Classify the function as linear, quadratic, or exponential.
f(x)=16^x
Answers
The given function f(x) = 16^x is an exponential function.
An exponential function is a mathematical function in which an independent variable appears in the exponent. In this case, the base of the function is 16, and the variable x is the exponent.
In the given function f(x) = 16^x, the variable x represents the exponent to which 16 is raised. As x increases, the function value grows rapidly, indicating exponential growth. The base of 16 signifies that the function is being multiplied by 16 for each unit increase in the exponent.
In contrast, a linear function has a constant rate of change, and a quadratic function has a squared term. The given function does not involve a linear relationship or a squared term, which confirms that it is not a linear or quadratic function.
Therefore, based on the given form f(x) = 16^x and the exponential growth nature of the function, we can classify it as an exponential function.
Learn more about exponential function here:
brainly.com/question/29287497
#SPJ11