Answers
Answer:
18
Step-by-step explanation:
If two people paint a wall, each will paint half of the sall
If jamie paints the entire wall in 54 minutes alone then he/she can paint half the wall in 54/2=27 minutes
The question said that it took 36 minutes all together, so if 27 minutes(jamies half) is subtracted from 36, we get that it took Connie 9 minutes for her half.
If connie paints an entire wall, then we multiply the time it took her( 9 minutes) by 2 to get 18 minutes.
Related Questions
A square rug has an area 77 ft2. Write the side length as a square root. Then decide if the side length is a rational number.
Answers
Answer:
s = √77
it is not rational since 77 not a perfect square
Step-by-step explanation:
area = s^2 = s * s = 77
==> s = √77
HELP!!!!!!!!!!!!!!!!!!

Answers
Answer:
D 0.89275
Step-by-step explanation:


Verify that ϕ(x)=2(1−cex), where cis an arbitrary constant, is a one-parameter family of solutions to dydx=y(y−2)2.Graph the solution curves corresponding to c=0,±1,±2using the same coordinate axes.
Answers
Answer:
Following are the solution:
Step-by-step explanation:
Given equation:
\(\frac{dx}{dy}= \frac{y(y-2)}{2}........(a)\)
\(\Phi (x) = \frac{2}{1-ce^x}\)
In the question \(\Phi (x)\), is a solution of the equation (a) only if when \(\Phi (x)\)satisfies equation (a):
let us find \(\Phi' (x)\):-
\(\Phi(x) =\frac{d}{dx} \Phi (x)=\frac{d}{dx}(\frac{2}{1-ce^x})\)
\(= 2 \frac{d}{dx}({1-ce^x}^-1)\\\\= 2 (-1) ({1-ce^x})^{-2} \frac{d}{dx}({1-ce^x})\\\\= -2 ({1-ce^x})^{-2} (-ce^x})\\\\= 2(-ce^x) ({1-ce^x})^{-2} \\\\\)
Now:
\(\frac{dy}{dx}=\frac{y(y-2)}{2}\\\\\frac{d}{dx}\Phi (x) =\frac{\Phi (x) (\Phi (x)-2)}{2}\\\)
by subtracting the value of \(\Phi (x)\)and \(\frac{d}{dx}\)\(\Phi (x)\),we get:
\(\to\)\(2ce^x(1-ce^x)^-2= \frac{(\frac{2}{1-ce^x})(\frac{2}{1-ce^x})^{-2}}{2}\)
\(=2ce^x (1-ce^x)^{-2}=\frac{1}{2}[\frac{2}{1-ce^x}(\frac{2-2(1-ce^x)}{1-ce^x)}]\\\\= \frac{1}{1-ce^x} \times \frac{2ce^x}{1-ce^x}\\\\=\frac{2ce^x}{(1-ce^x)^2}\\\\=2ce^x (1-ce^x)^-2\)
\(\bold{2ce^x(1-ce^x)^-2=2ce^x(1-ce^x)^-2}\)
\(\Phi (x)\) the solution of the given equation. \(\Phi (x)\) has one Parameter Family of
\(\frac{dy}{dx}=\frac{y(y-2)}{2}\)
\(\Phi (x) =\frac{2}{1-ce^x}\\\\_{when} \ \ \ c= 0 \to \Phi (x) =\frac{2}{1-0\times e^x}=2\\\\_{when} \ \ \ c= 1 \to \Phi (x) =\frac{2}{1-1\times e^x}=\frac{2}{1-e^x}\\\\_{when} \ \ \ c= -1 \to \Phi (x) =\frac{2}{1-(-1)\times e^x}=\frac{2}{1+e^x}\\\\_{when} \ \ \ c= 2 \to \Phi (x) =\frac{2}{1-(-2)\times e^x}=\frac{2}{1-2e^x}\\\\_{when} \ \ \ c= -2 \to \Phi (x) =\frac{2}{1-(-2)\times e^x}=\frac{2}{1+2e^x}\\\\\)

15 less than 3 times a number is 5 more than half of the number.
Answers
Answer:
Mystery Number is 8
Step-by-step explanation:
3x - 15 = 5 + 1/2x
3x - 1/2x = 15 + 5
5/2x = 20
x = 20 / 5/2
x = 20 * 2/5
x = 40 / 5
x = 8
Mario constructs a scale model of a building with a rectangular base. His model is 4.2 inches in length and 2 inches in width. The scale of the model is 1 inch = 15 feet.
What is the actual area, in square feet, of the base of the building?
Answers
The actual base of the building is 1890 square feet.
What is a rectangle?A rectangle is a two-dimensional figure with length and width.
The area of a rectangle is Length x width.
We have,
1 inch = 15 feet
Rectangular base:
Length = 4.2 in
Width = 2 in
So,
4.2 in = 4.2 x 15 feet = 63 feet
2 in = 2 x 15 = 30 feet
Now,
The actual base of the building.
= 63 x 30
= 1890 square feet
Thus,
1890 square feet.
Learn more about rectangles here:
https://brainly.com/question/15019502
#SPJ9
If z varies inversely as w?, and z = 20 when w=6, find z when w=4.
Answers
Answer:
\(z = \frac{5}{6}\)
Step-by-step explanation:
\(z\) ∝ \(\frac{k}{w}\)
Where k is a constant we need to find when solving these questions.
\(20 = \frac{k}{6}\)
\(k = \frac{10}{3}\)
\(z = \frac{10/3}{4}\)
\(z = \frac{5}{6}\)
Use the diagram to find the measures of all the angles, given that m<1 = 76º.

Answers
Answer:
m<2 = 104º
m<3 = 76º
m<4 = 104º
Step-by-step explanation:
given: m<1 = 76º
m<3 = m<1 this is because they are opposite angles which equals each other
A straight line = 180º
so m<1 + m<2 = 180 and m<3 + m<4 = 180
m<2 = 180 - m<1
m<2 = 180 - 76
m<2 = 104º
m<2 = m<4 so m<4 is also 104º
Hope this helps, Let me know if you have any questions !
m∠1 = 76° Given.
m∠1 ≅ m∠3 Vertical Angle theorem.
m∠3 = 76° CPCTC
m∠1 + m∠2 = 180° (supplementary angles)
m∠3 + m∠2 = 180° (supplementary angles)
m∠1 & m∠3 ∴ Congruent (congruent supplements theorem)
m∠2 + m∠3 = 180° (supplementary angles)
m∠4 + m∠3 = 180° (supplementary angles)
m∠2 & m∠4 ∴ Congruent (congruent supplements theorem)
∴ IF m∠1 = 76° (Given)
THEN:
m∠2 = 104° (Supplementary angles)
m∠3 = 76° (Definition of vertical angles)
m∠4 = 104° (Supplementary angles)
Please someone help me with this

Answers
Answer:
2,-1.5
Step-by-step explanation:
To find the midpoint of a line segment, take the average of the x coordinates and y coordinates of the two points that make it up.
\(\frac{2+2}{2} ,\frac{4+(-7)}{2}\)
=\(\frac{4}{2} , \frac{-3}{2}\)\(\frac{4}{2} , \frac{-3}{2}\)
=2,-1.5
Here's the answer for you

Fidgets cost $3 each and Pop Its cost $4 each. If you buy a total of 20 Fidgets and Pop
Its for $75, which system of equations could you use to determine how many of each
you bought? Let x represent the number of fidgets you bought and y represent the
number of pop its you bought.
Answers
The number of fidgets and pop bought was 15 each
How to determine the equationFrom the information given, we have that;
1 fidget costs $3
1 Pop cost $4
Let the number of Fidgets be x
Let the number of Pop be y
Then, we have that a total of 20 fidgets and Pop cots $75
We have that;
20x + y = 75
Now, substitute the value of x as 3, we get;
20(3) + y= 75
expand the bracket
y = 75 - 60
y = 15
The number of fidgets is expressed as;
20x/4 = 20(3) /4 = 15
Learn more about linear equations at: https://brainly.com/question/2030026
#SPJ1
Completely factor the given polynomial, if possible. If the polynomial cannot be factored, indicate "Not Factorable".
cq+cw+qy+wy
Answers
The requried completely factored form of the given polynomial is (q+w)(c+y).
We can group the first two terms and the last two terms together, then factor out the common factors:
= cq+cw+qy+wy
= c(q+w) + y(q+w)
= (q+w)(c+y)
Therefore, the completely factored form of the given polynomial is (q+w)(c+y).
Learn more about the factorization of polynomials here:
https://brainly.com/question/28315959
#SPJ1
Ok here go a few of them

Answers
Answer:
1 = 58°
2 = 32°
3 = 32°
Step-by-step explanation:
Charity is ordering a sundae at a restaurant, and the server tells her that she can have up to five toppings: chocolate chips, butterscotch sauce, strawberries, a cherry, and hot fudge. Since she cannot decide how many of the toppings she wants, she tells the server to surprise her. If the server randomly chooses which toppings to add, what is the probability that Charity gets just chocolate chips and a cherry? Express your answer as a fraction or a decimal number rounded to four decimal places.
Answers
Answer:
1/31 = 0.0323 probability that Charity gets just chocolate chips and a cherry.
Step-by-step explanation:
A probability is the number of desired outcomes divided by the number of total outcomes.
Number of subsets in a set of n elements:
The number of subsets in a set of n elements, including the empty set, is given by:
\(2^{n}\)
Up to five toppings:
Up to five toppings means that the total number of possibilities is:
\(T = 2^{5} - 1 = 32 - 1 = 31\)
We subtract one to disconsider the option with no toppings.
What is the probability that Charity gets just chocolate chips and a cherry?
Chocolate chips and cherry is 1 subset, so \(D = 1\)
The probability is:
\(p = \frac{D}{T} = \frac{1}{31} = 0.0323\)
1/31 = 0.0323 probability that Charity gets just chocolate chips and a cherry.
Does anyone know this?
Answers:
A. b=4/3, c=12
B. b=4/3, c=2/3
C. b=8/3, c=16/3
D. b=8/3, c=16

Answers
Answer:
the answer will be choice D
as we can see that the triangle have angles measuring 30 60 and 90 so we will use the 30-60-90 rule
you can look up the explantion about the rule online
A new cylindrical can with a diameter of 4cm is being designed by a local company. The surface area of the can is 140 square centimeters. What is the height of the can? Estimate using 3.14 for pi and round to the nearest hundredth. Apply the formula for the surface area of a cylinder SA=2B+Ph
Answers
The height of the can of cylinder shape is 9.14 cm.
What is a cylinder?
In mathematics, a cylinder is a three-dimensional solid that maintains two parallel bases separated by a curved surface at a specific distance. These bases frequently have a circular shape (like a circle), and an axis connects their respective centres.
We are given the diameter as 4 cm.
So, the radius is 2cm.
Also, it is given that the surface area of the can is 140 square centimeters.
So, using the surface area of cylinder, we get
⇒Area = 2πr (h + r)
⇒140 = 2π * 2 (h + 2)
⇒140 = 4π (h + 2)
⇒140 = 4 * 3.14 * (h + 2)
⇒140 = 12.56 * (h + 2)
⇒11.14 = h + 2
⇒h = 9.14
Hence, the height of the can of cylinder shape is 9.14 cm.
Learn more about cylinder from the given link
https://brainly.com/question/27440983
#SPJ1
HELP GEOMETRY PROOFS

Answers
Step-by-step explanation:
See the attached for the proof

The Bears has 17 in tide two of the last 13 games they have not for filled any games which ratio correctly compares their wins to losses (I WILL MARK BRAINLEIST)
Answers
Please awnser asap I am
Stuck

Answers
Answer:
it is too blury to read
Step-by-step explanation:
Can someone help me please

Answers
Answer:
options 2, 3 and 5
Step-by-step explanation:
first of all, because
n²+3n+2n = 6n simplifies to n²+5n = 6n, which simplifies to
n² = n, which is not true for all n not equal to 0 or 1.
option 6 is not a valid reason, as it made a calculation error.
options 1 and 4 make invalid simplifications.
In a certain section of Southern California, the distribution of monthly rent for a one-bedroom apartment has a mean of $2,275 and a standard deviation of $290. The distribution of the monthly rent does not follow the normal distribution. In fact, it is positively skewed. What is the probability of selecting a sample of 65 one-bedroom apartments and finding the mean to be at least $2,095 per month
Answers
Answer:
100% probability of selecting a sample of 65 one-bedroom apartments and finding the mean to be at least $2,095 per month
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
Mean of $2,275 and a standard deviation of $290.
This means that \(\mu = 2275, \sigma = 290\)
Sample of 65:
This means that \(n = 65, s = \frac{290}{\sqrt{65}}\)
Finding the mean to be at least $2,095 per month
This is 1 subtracted by the p-value of Z when X = 2095. So
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{2095 - 2275}{\frac{290}{\sqrt{65}}}\)
\(Z = -5\)
\(Z = -5\) has a p-value of 0.
1 - 0 = 1
100% probability of selecting a sample of 65 one-bedroom apartments and finding the mean to be at least $2,095 per month
Solve (x+1)2 =13/4 using the square root property
Answers
Answer:
Starting with the equation:
(x + 1)^2 = 13/4
We can use the square root property, which states that if a^2 = b, then a is equal to the positive or negative square root of b.
Taking the square root of both sides, we get:
x + 1 = ±√(13/4)
Simplifying under the radical:
x + 1 = ±(√13)/2
Now we can solve for x by subtracting 1 from both sides:
x = -1 ± (√13)/2
Therefore, the solutions to the equation are:
x = -1 + (√13)/2 or x = -1 - (√13)/2
Step-by-step explanation:
I need help with this please
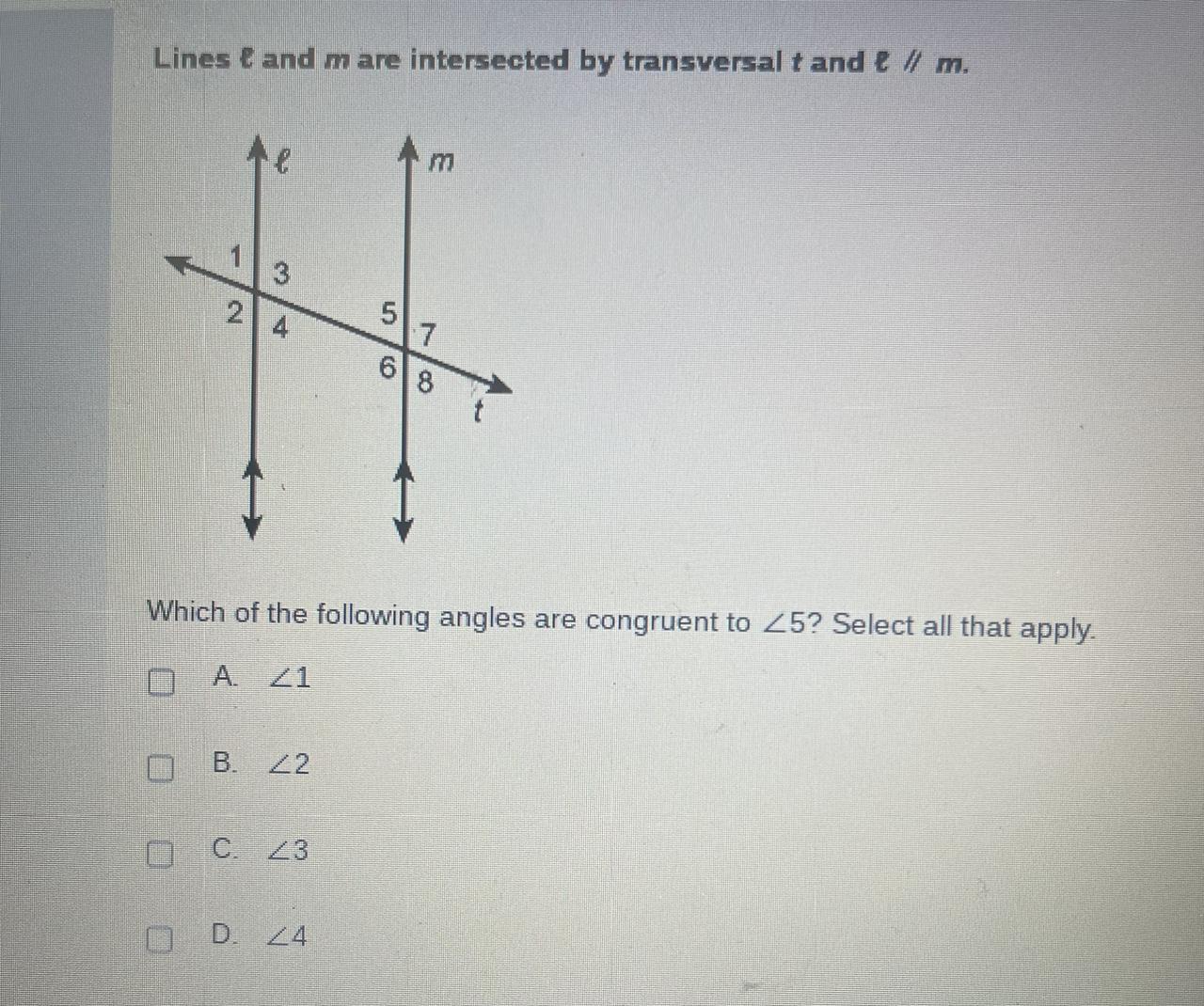
Answers
Answer:
<4 (D)
Step-by-step explanation:
it is the same angle :D
also can you please help me??
At a certain high school, the Prom Committee is going to choose new members. There are 10 students from the Junior class and 3 students from the Senior
class who are willing to be new members. In how many ways can 7 new members be chosen if 2 or fewer must be from the Senior class?
Answers
The number of ways that 7 new members be chosen if 2 or fewer must be from the Senior class is; 705 ways
How to solve permutation and combination?The formula for probability combination is;
nCr = n!/(r! * (n – r)!)
where;
n is the total number of items.
r is the number of things that may be selected at one time.
The number of ways that 2 students can be selected from the senior class is;
N(2 students from the SR class) = 3C2 * 10C2 = 135 ways
Similarly;
N(1 student from the SR class) = 3C1 * 10C3 = 360
N(0 students from the SR class) = 3C0 * 10C4 = 210
Thus, number of ways that 7 new members be chosen if 2 or fewer must be from the Senior class is;
135 + 360 + 210 = 705 ways
Read more about permutation and combination at; https://brainly.com/question/4658834
#SPJ1
When an object is weighed on a scale, the number displayed may vary from the object’s actual weight by at most 0.4 pounds. The scale says the object weighs 125.8 pounds. Part A: Write an absolute value inequality that describes the range of the actual weight of the object. Use the variable w to represent the actual weight of the object. Part B: Solve the absolute value inequality for w. Express your answer as a compound inequality.
Answers
The compound inequality that represents the range of the actual weight of the object is 125.4 ≤ w ≤ 126.2.
Part A: The absolute value inequality that describes the range of the actual weight of the object is:
|w - 125.8| ≤ 0.4
Part B: To solve the absolute value inequality, we can break it down into two separate inequalities:
w - 125.8 ≤ 0.4 and - (w - 125.8) ≤ 0.4
Solving the first inequality:
w - 125.8 ≤ 0.4
Add 125.8 to both sides:
w ≤ 126.2
Solving the second inequality:
-(w - 125.8) ≤ 0.4
Multiply by -1 and distribute the negative sign:
-w + 125.8 ≤ 0.4
Subtract 125.8 from both sides:
-w ≤ -125.4
Divide by -1 (note that the inequality direction flips):
w ≥ 125.4
Combining the solutions, we have:
125.4 ≤ w ≤ 126.2
The object is 125.4 ≤ w ≤ 126.2.
for more questions on compound
https://brainly.com/question/3989769
#SPJ8
Out of 20 people how many would you expect to say that they like all seasons
Answers
Answer:
None
Step-by-step explanation:
Truly, I'm not sure what type of problem this is, but most people don't favor all the seasons. If there is more to the problem, I would be glad to help further.
Answer:
One possible way to estimate how many people out of 20 would say that they like all seasons is to use a simple random sample. A simple random sample is a subset of a population that is selected in such a way that every member of the population has an equal chance of being included. For example, one could use a random number generator to assign a number from 1 to 20 to each person in the population, and then select the first 20 numbers that appear. The sample would then consist of the people who have those numbers.
Using a simple random sample, one could ask each person in the sample whether they like all seasons or not, and then calculate the proportion of positive responses. This proportion is an estimate of the true proportion of people in the population who like all seasons. However, this estimate is not exact, and it may vary depending on the sample that is selected. To measure the uncertainty of the estimate, one could use a confidence interval. A confidence interval is a range of values that is likely to contain the true proportion with a certain level of confidence. For example, a 95% confidence interval means that if the sampling procedure was repeated many times, 95% of the intervals would contain the true proportion.
One way to construct a confidence interval for a proportion is to use the formula:
p ± z * sqrt(p * (1 - p) / n)
where p is the sample proportion, z is a critical value that depends on the level of confidence, and n is the sample size. For a 95% confidence interval, z is approximately 1.96. For example, if out of 20 people in the sample, 12 said that they like all seasons, then the sample proportion is 0.6, and the confidence interval is:
0.6 ± 1.96 * sqrt(0.6 * (1 - 0.6) / 20)
which simplifies to:
0.6 ± 0.22
or:
(0.38, 0.82)
This means that we are 95% confident that the true proportion of people who like all seasons in the population is between 0.38 and 0.82. Therefore, based on this sample and this confidence interval, we would expect between 8 and 16 people out of 20 to say that they like all seasons in the population.
MARK AS BRAINLIEST!!!
Drag the tiles to the correct boxes to complete the pairs.

Answers
Answer:
Here you go. Check attached figure
Step-by-step explanation:

Solve 8W + 20 = 4
How do you solve this equation?
Answers

Answer:
W = -2
Step-by-step explanation:
8W + 20 = 4
=> 8W = 4 - 20
=> 8W = -16
=> W = -16 / 8
=> W = -2
Hope it helps :)
Please mark my answer as the brainliest
State sales tax is 3%. How much would you pay on a $246 pair of shoes?
Round your answer to the nearest cent.
Answers
Answer:
Step-by-step explanation:
246(.03)= 7.38
246+7.38= $253.38
1. Working on a circle of radius 10cm, explain in detail how to determine the values of each of the following trigonometric expres- sions. Include a picture for each to help with your explanations.
(a) cos(5π)
(b) sin(−9π/2)
(c) sin(183π/2)
2. Approximate the value of cos π◦. Explain your reasoning. Do not use a calculator. Include a picture to help with your explanation.
Answers
The x-coordinate of this point is -1, so cos(5π) = cos(900 degrees) = -1.
The y-coordinate of this point is -1, so sin(-9π/2) = sin(-810 degrees) = -1.
The y-coordinate of this point is 1, so sin(183π/2) = sin(16,470 degrees) = 1.
How to calculate the valueIt should be noted that go find cos(5π), we first need to convert 5π to degrees. We know that π radians is equal to 180 degrees, so 5π radians is equal to 5π × (180/π) = 900 degrees. The x-coordinate of this point is -1, so cos(5π) = cos(900 degrees) = -1.
Also, to find sin(-9π/2), we first need to convert -9π/2 to degrees. We know that π radians is equal to 180 degrees, so -9π/2 radians is equal to -9π/2 × (180/π) = -810 degrees. The y-coordinate of this point is -1, so sin(-9π/2) = sin(-810 degrees) = -1.
Learn more about coordinate on
https://brainly.com/question/17206319
#SPJ1

Which number is closest to 1
A. 0.987
b. 0.111
c.0.561
d. 0.786
Answers
Answer:
Letter A
Step-by-step explanation:
Just think: which number would have the greatest value if it was rounded to the nearest hundredth
Answer: A
Step-by-step explanation:
I think the answer is correct becuase, If we taken all the numbers and put them on a number line they would all be under one. But when we look at the number line we would see that .987 is the closest because it is almost a whole number. And even if we did it without the number line what ever number we see that has the greatest digit and its in the negatives thats the closest to one. (I hope what I said makes sense!)
Hope This Helps!
What is the y-value in the solution to this system of linear equations?
4x + 5y = −12
-2x + 3y = −16
−4
−2
2
5What is the y-value in the solution to this system of linear equations?
4x + 5y = −12
-2x + 3y = −16
−4
−2
2
5
Answers
Answer:
The answer is the first one: -4 on Edge
Step-by-step explanation:
The y-value of the solution to the system of linear equations given is: A. -4.
How to Find the Solution to the System of Linear Equations?Given two linear equations, such as:
4x + 5y = −12 --> Eqn. 1
-2x + 3y = −16 --> Eqn. 2
Multiply eqn. 1 by 2 and eqn. 2 by 4
8x + 10y = −24 --> Eqn. 3
-8x + 12y = −64 --> Eqn. 4
Add to eliminate x
22y = -88
22y/22 = -88/22
y = -4
The y-value of the solution is: A. -4.
Learn more about the solution of a system of linear equations on:
https://brainly.com/question/2226590
#SPJ9
