Find a formula for the nth partial sum of this Telescoping series and use it to determine whether the series converges or diverges. (pn)-² Σ 2 3 2+2+1 n=1n² n
Answers
The given series is a telescoping series, and we can find a formula for the nth partial sum by simplifying the terms and canceling out the telescoping terms.
The given series is ∑(n=1 to ∞) (2/n^2 - 2/(n+1)^2 + 1/n). To find the nth partial sum, we simplify the terms by combining like terms and canceling out the telescoping terms:
S_n = (2/1^2 - 2/2^2 + 1/1) + (2/2^2 - 2/3^2 + 1/2) + ... + (2/n^2 - 2/(n+1)^2 + 1/n)
We can observe that most terms in the series cancel each other out, leaving only the first and last terms:
S_n = 2/1^2 + 1/n
Simplifying further, we get:
S_n = 2 + 1/n
As n approaches infinity, the term 1/n approaches zero. Therefore, the nth partial sum S_n approaches 2. Since the nth partial sum converges to a finite value (2), the series converges.
To learn more about telescoping series click here :
brainly.com/question/32389173
#SPJ11
Related Questions
Admission to a science museum is $22 for an adult. The cost for a child is $5 less than the cost for an adult. What would be the total cost of admission for 12 adults and 15 children? Explain.
Answers
Answer:
The total cost is 519
Step-by-step explanation:
22x12=264 and 22-5=17 so 17x15=255
264+255= 519
what is the equation of a line parallel to y=3x-2 and goes through the point (-1,1)
Answers
Answer:
y = 3 x − 29
Step-by-step explanation:
First, let's find the slope of the line
y = 3 x + 2
As the equation is already in slope-intercept form
y = m x + c
Slope = 3
Let a point ( x , y ) be on the new line.
By finding the slope again,
y − 1 x − 10 = 3
y − 1 = 3 ( x − 10 )
y − 1 = 3 x − 30
Which can then be converted to different forms:
Standard form:
3 x − y = 29
Equation form:
3 x − y−29 = 0
Slope-intercept form:
y = 3 x − 29
graph{3x-y=29 [-32.3, 47.7, -34.1, 5.9]}
A store sells applesauce in two sizes.
Answers
Answer:
Could u give us more info in ur question pls?
please help, thanks if you do

Answers
Answer:
Pretty sure it's B. 1
Step-by-step explanation:
y = mx + b is y-intercept form and B is usually where you put the first dot on the y axis, and that is positive 1, as you can see on the graph.
Hope you get a good grade! :)
can someone help me with these kind of fractions
\(\frac{1}{2} of \frac{2}{3}\)
Answers
Answer:
\(\frac{2}{6}\) or \(\frac{1}{3}\)
Step-by-step explanation:
To find a fraction of a fraction simply multiply the numerators and denominators into another fraction:
\(\frac{1}{2}*\frac{2}{3} = \frac{2}{6} = \frac{1}{3}\)
Answer:
1/3.
Step-by-step explanation:
'of' means multiply. so
1/2 of 2/3
= 1/2 * 2/3
= 1*2 / 2*3
= 2/6
= 1/3.
help ASAP ill mark brainliest

Answers
Mean = 16.090909090909
Median = 16
Mode = 16
Range = 5
Mean ⎯⎯⎯
x
¯
16.090909090909
Median ˜
x
~
16
Mode 16
Range 5
Minimum 14
Maximum 19
Count n 22
Sum 354
Quartiles Quartiles:
Q1 --> 15
Q2 --> 16
Q3 --> 17
Interquartile
Range IQR 2
Outliers none
Answer:
16.1, 16, 16
Step-by-step explanation:
1) we are going to do the mean :)
you add all the number together and divide by the same number
you should get 354/22 which is 16.0909....... since its round to tenth place, we place it at 16.1.
2) median, for this one, you have to lay out the numbers and see which one is in the middle, in 14,15,16,17,19, 16 is the median.
3) the number that appear the most is the mode, so right now we have
three 17s and six 16s, don't worry about the others because its not in the answer choice, so its 16.
Hope this helps :D
Which of the following expressions could be equal to f(x)???

Answers
The average time to serve a customer at a fast-food restaurant is 5 minutes. The standard deviation of the service time is 4 minutes. What is the coefficient of variation of the service time
Answers
=13.62
step-by-step explanation- We are given the interarrival time (a = 15 min), service time (p = 20 min), number of servers (m = 3 people), standard deviation of interarrival time (15 min) and standard deviation of service time (60 min). - Therefore, the coefficient of variation of arrival times is 15 / 15 = 1 and the coefficient of variation of service times is 60 / 20 = 3. Moreover, the utilization is 20 / (15 x 3) = 0.4444. Therefore, the average time in the queue is 6.6667 x 0.4086 x 5.0 = 13.6211 minutes, or 13.62 minutes rounded to two decimals
- We are given the interarrival time (a = 15 min), service time (p = 20 min), number of servers (m = 3 people), standard deviation of interarrival time (15 min) and standard deviation of service time (60 min). - Therefore, the coefficient of variation of arrival times is 15 / 15 = 1 and the coefficient of variation of service times is 60 / 20 = 3. Moreover, the utilization is 20 / (15 x 3) = 0.4444. Therefore, the average time in the queue is 6.6667 x 0.4086 x 5.0 = 13.6211 minutes, or 13.62 minutes rounded to two decim
Emma's luggage may be lost with probability p = 0.1. The luggage and its content are estimated to be worth 316.05. Emma's utility insure against the loss of the luggage, what is the maximum insurance premium I that Emma would be willing to pay?
Answers
Emma's luggage may be lost with probability p = 0.1. The luggage and its content are estimated to be worth 316.05. Emma's utility insures against the loss of the luggage. What is the maximum insurance premium I that Emma would be willing to pay?
Solution:To calculate Emma's maximum insurance premium, let's start by calculating her expected utility if she doesn't insure her luggage.U (no insurance) = 0.9 x U (316.05) + 0.1 x U (0)where U (316.05) is Emma's utility function for 316.05 value, and U (0) is Emma's utility function for a loss of the luggage. Emma has not insured her luggage, hence, if it gets lost, she will get 0 value for it.A sum of 316.05 is worth more than 0, Emma will still get a certain amount of utility, which will be larger than 0.
Therefore, Emma's utility function is likely to be positive, so let us assume that U (0) = 0.If we plug this information into the above equation, we will have:U (no insurance) = 0.9U (316.05) + 0.1 × 0 = 0.9U (316.05)Hence, Emma's expected utility, if she doesn't insure her luggage, will be 0.9U (316.05).However, if Emma chooses to insure her luggage, she will pay the insurance premium I. If the luggage gets lost, she will get reimbursed by the insurance company for 316.05. Her expected utility function, if she insures her luggage, will be:
U (insurance) = 0.9U (316.05 – I) + 0.1U (316.05)Where U (316.05 – I) is Emma's utility function for 316.05 – I value. Emma will get this amount if the luggage is not lost, but she has to pay the premium I.If we compare Emma's expected utility when she insures her luggage and when she doesn't insure her luggage, we will have the following inequality:
U (insurance) ≥ U (no insurance)0.9U (316.05 – I) + 0.1U (316.05) ≥ 0.9U (316.05)Let us solve this inequality:0.9U (316.05 – I) + 0.1U (316.05) ≥ 0.9U (316.05)0.9U (316.05 – I) ≥ 0.8U (316.05)U (316.05 – I) ≥ 0.89U (316.05)Since U (316.05 – I) is a decreasing function, it will get smaller as I gets larger.
Hence, to maximize Emma's expected utility, we need to minimize the insurance premium I that she pays to the insurance company.If Emma doesn't insure her luggage, her expected utility will be 0.9U (316.05)Emma will choose to insure her luggage if her expected utility is larger if she insures her luggage.U (insurance) = 0.9U (316.05 – I) + 0.1U (316.05)0.9U (316.05 – I) ≥ 0.8U (316.05)U (316.05 – I) ≥ 0.89U (316.05)Emma will choose to insure her luggage if her expected utility is larger if she insures her luggage. Hence,Emma's maximum insurance premium I that Emma would be willing to pay is $31.35.
If Emma chooses to insure her luggage, she will pay the insurance premium I. Her expected utility function, if she insures her luggage, will be U (insurance) = 0.9U (316.05 – I) + 0.1U (316.05). Emma will choose to insure her luggage if her expected utility is larger if she insures her luggage. Therefore, Emma's maximum insurance premium I that Emma would be willing to pay is $31.35. The utility function is considered decreasing as Emma has to pay more premium.
To know more about utility function :
brainly.com/question/30652436
#SPJ11
Lauren’s book is 180 pages long. She has read 80% of it. How many pages has she read?
Answers
Answer:
144 pages read
Step-by-step explanation:
80% = 0.8
0.8 * 180 = 144
Aidan and Godwin like saving money when grocery shopping by sharing the costs. Aidan buys 10 cans of soup for $8.69 and a case of (24 cans) of chili for $19.20. Godwin takes 4 cans of soup and 12 cans of chili. Not including sales tax, how much does Godwin owe Aidan?
Calculate the unit rate of the soup
What is the unit rate of the soup?
Calculate the unit rate of the chili
What is the unit rate of the chili?
How much does Godwin owe Aidan?
Answers
Answer: To find how much Godwin owes Aidan, we first need to calculate the total cost of the items Aidan purchased:
10 cans of soup for $8.69, so the cost per can of soup is $8.69/10 = $0.869 per can.
1 case of chili for $19.20, so the cost per can of chili is $19.20/24 = $0.80 per can.
Godwin takes 4 cans of soup at $0.869 per can, which is a total of 4 x $0.869 = $3.476 for the soup.
Godwin takes 12 cans of chili at $0.80 per can, which is a total of 12 x $0.80 = $9.60 for the chili.
Therefore, Godwin owes Aidan $3.476 + $9.60 = $13.076.
The unit rate of the soup is $0.869 per can.
The unit rate of the chili is $0.80 per can.
Step-by-step explanation:
Find the perimeter and area of the
polygon with the given vertices.
W(5, — 1), X(5, 6), Y(2, — 1), Z(2, 6)
The perimeter is units. The area is
squareunits.
Answers
The perimeter of the polygon will be 20 units and the area will be 21 square units.
From the given vertices a rectangle will be formed. A rectangle is a closed figure in which each interior angle is a right angle. The Perimeter of the rectangle can be given by formula 2(l + b) and the area is given by l×b where l is the length and b is breadth of rectangle. Now from the given points the dimensions of rectangle will follow the order W (5, -1), X (5, 6), Z (2, 6) and Y (2, -1).
The length of the rectangle is given by l = √ (6 + 1) ² + (5 - 5) ²
l = √49
l = 7 units
The breadth of the rectangle is given by b = √ (6 - 6) ² + (2 - 5) ²
b = √9
b = 3 units
Now, the perimeter of rectangle = 2 (l + b)
P = 2(7 + 3)
P = 20 units
Area of the rectangle = l×b
A = 7×3
A = 21 square units.
Thus, the perimeter and area are 20 units and 21 square units respectively.
Learn more about Polygon at:
brainly.com/question/12622435
#SPJ9

In 1992, the moose population in a park was measured to be 3590. by 1999, the population was measured again to be 4500. if the population continues to change linearly p(t)= ____ b.) what does your model predict the moose population to be in 2006?
Answers
population at 1992 = 3590
Population after Seven years (1999) = 4500
Given two points (t1, P1) and (t2, P2), the slope of the line m can be found.
p1 = (1992, 3590) and p2 = (1999, 4500)
m= ΔP/Δt
m= ((4500-3590))/((1999-1992))
m = 910/7
m=130 is the slope
The linear population function P(t) is
P(t)=130t + P0
Find the Y-Intercept P0
The population function P(t) is measured since the year 1990, year zero. The first moose population was measured in 1992, one year later. This provides an initial condition P (1) = 4500.
P (1) =130 (1) + P0 = 4500
P0 = 4370
P(t)=20t+4630
The moose population P(t) changes linearly year after year. The population function P(t) is measured in terms of t years since 1990.
t= 1990, P (0) =4370
t =1992, P (1) =130 (1) + 4370 = 4500 matches data
t=1999, P (2) = 130(2) + 4370 = 4630
t=2006, P (3) = 130(3) + 4370 = 4760
To learn more about linear population change . Click, https://brainly.com/question/24078838
#SPJ4
John weighed 156 pounds give or take 8 pounds, ten years ago.
Write the absolute value inequality representing the range of John's weight.
Answers
The absolute value of inequality representing the range of John's weight is | x - 156 | ≤ 8.
What is absolute value of inequality?An absolute value inequality is an inequality that contains an absolute value expression. The absolute value of a number represents the distance between that number and zero on a number line.
What is absolute value expression?An absolute value expression is a mathematical expression that contains an absolute value function, denoted by vertical bars around a number or expression. The absolute value of a number is its distance from zero on a number line, so an absolute value expression represents a positive number, regardless of whether the original number was positive or negative.
As per the given question,
If John weighed 156 pounds give or take 8 pounds ten years ago, then his weight could have been anywhere from 156 - 8 = 148 pounds to 156 + 8 = 164 pounds.
To write this as an absolute value inequality, we can let x represent John's weight, and use the absolute value to represent the distance from the mean weight of 156 pounds. The inequality would be:
| x - 156 | ≤ 8
This inequality says that the distance between John's weight (x) and the mean weight of 156 pounds must be less than or equal to 8 pounds. In other words, John's weight must be within 8 pounds of 156, which represents the range of possible weights he could have had ten years ago.
To know more about absolute value inequality, visit:
https://brainly.com/question/30201926
#SPJ1
How do I solve this ?

Answers
Answer:
Step-by-step explanation:
I'm just going to go out on a limb here and assume that those are a set of poorly made parenthesis. This, then, would be your equation:
\(x+\frac{x}{7}+\frac{1}{11}(x+\frac{x}{7})=60\)
The first thing to do is distribute through the parenthesis to get:
\(x+\frac{x}{7}+\frac{x}{11}+\frac{x}{77}=60\)
Next is to get rid of the denominators by multiplying by the LCM of 77:
\(77(x+\frac{x}{7}+\frac{x}{11}+\frac{x}{77}=60)\) which gives you:
77x + 11x + 7x + x = 4620 and
96x = 4620 so
\(x=\frac{385}{8}\)
subway sells foot long sandwiches that have a mean of 11 inches and a standard deviation of .5 inches. 20% of sandwiches are less than inches. (the cumulative standardized normal distribution table indicates a z value of -.84 for 20%) 11.500 11.42 10.58 cannot be determined from the information given
Answers
using standard z value, 20% of sandwiches are less than 10.58 inches.
In the given question,
Subway sells foot long sandwiches that have a mean of 11 inches and a standard deviation of 0.5 inches.
20% of sandwiches are less than...............inches.
The cumulative standardized normal distribution table indicates a z value of -0.84 for 20%.
From the question we know that
Mean(μ) = 11 inches
Standard Deviation(σ) = 0.5 inches
We have to find less than of 20% of sandwiches for z value of -0.84
P(ƶ<z) = 20%
We can write it as
P(ƶ<-0.84) = 20/100
P(ƶ<-0.84) = 0.20
Since z = -0.84
X-μ/σ = -0.84
Now putting the value
X-11/0.5 = -0.84
Multiply by 0.5 on both side
X-11/0.5 *0.5= -0.84*0.5
X-11= -0.42
Add 11 on both side
X-11+11= -0.42+11
X = 10.58
Hence, 20% of sandwiches are less than 10.58 inches.
To learn more about standard z value link is here
https://brainly.com/question/27315585
#SPJ4
Right question is here
Subway sells foot long sandwiches that have a mean of 11 inches and a standard deviation of 0.5 inches. 20% of sandwiches are less than ................. inches. (The cumulative standardized normal distribution table indicates a z value of -.84 for 20%)
(a) 11.500
(b) 11.42
(c) 10.58
(d) cannot be determined from the information given
how much work is done when a 100 lb rock is lifted to a height of 3 ft?
Answers
A. The work done is 300 ft-lbs when a 100 lb rock is lifted to a height of 3 ft.
To calculate the work done, we can use the formula: Work = force x distance x cos(Ф).In this case, the force is the force of gravity acting on the rock, which can be calculated using the formula:
force = m * g
where m is the mass of the rock and g is the acceleration due to gravity (32.17 ft/s^2).
force = 100 lb * 32.17 ft/s^2 = 3,217 ft-lbs
The distance is the height to which the rock is lifted, which is 3 ft.
The angle of the rock to the vertical is 90 degrees, so cos(90) = 0.
So,
Work = force x distance x cos(theta) = 3,217 ft-lbs * 3 ft * 0 = 300 ft-lbs
So, the work done is 300 ft-lbs.
For more questions like Work done click the link below:
https://brainly.com/question/13662169
#SPJ4
What is sextillion divided by nonmillion times 10,000 minus 200 million plus 5000.
Answers
The answer to this arithmetic expression is approximately 9.9998 x 10¹⁸
Define the term expression?A combination of numbers, variables, and operators that represents a quantity or mathematical relationship is called an expression.
First, divide sextillion (10²¹) by nonmillion (10⁶) to get 10¹⁵.
Next, multiply 10¹⁵ by 10,000 to get 10¹⁹.
Subtract 200 million (2 x 10⁸) from 10¹⁹ to get 9.9998 x 10¹⁸.
Finally, add 5,000 to get the result of approximately 9.9998 x 10¹⁸ + 5,000 = 9.9998 x 10¹⁸ + 0.0005 x 10¹⁸ = 9.9998 x 10¹⁸.
Therefore, the answer to this arithmetic expression is approximately 9.9998 x 10¹⁸
To know more about expression, visit:
https://brainly.com/question/1859113
#SPJ1
4x = 18 as an improper fraction in its simplest form?
Answers
Answer:
x = 9/2
Step-by-step explanation:
4x = 18
divide the 4 on both sides so it equals
x = 18/4
then simplify it to
x = 9/2
sample size and the confidence level width have a (n) __________ relationship.
Answers
Sample size and the confidence level width have an inverse relationship. As the sample size increases, the confidence level width decreases.
When determining a confidence interval for a population parameter, such as the mean or proportion, a larger sample size provides more information about the population. This increased information leads to a narrower confidence interval.
The confidence level width is influenced by two factors: the sample standard deviation (or the variability of the data) and the critical value associated with the desired confidence level. As the sample size increases, the sample standard deviation becomes a more accurate estimate of the population standard deviation. This reduces the variability and leads to a narrower confidence interval.
A larger sample size leads to a decrease in the confidence level width, providing a more precise estimate of the population parameter with a higher level of confidence.
Learn more about ”confidence interval” here:
brainly.com/question/32546207
#SPJ11
help me solve please show steps

Answers
There can be several possibilities and causes
y>2x-1
Then line will be dashed and solution region to be shaded.y<2x-1
Same like beforey≤2x-1
Solid line should be done and shading the solution regiony≥2x-1
Same like beforey=2x-1
A straight line and no shadingCredit: Mister Brainly
There can be several possibilities and causes:
y>2x-1
Then line will be dashed and solution region to be shaded.
y<2x-1
Same like before
y≤2x-1
Solid line should be done and shading the solution region
y≥2x-1
Same like before
y=2x-1
A straight line and no shading
Why is the power of 2 called square?
Answers
The power of 2 is called a square due to the definition of the area of a square.
What are a square and Power?
A square is a quadrilateral with four equal sides and four equal angles that is a regular quadrilateral. The square's angles are at a straight angle or 90 degrees. The square's diagonals are also equal and split at a 90-degree angle.
The base number is the factor that is multiplied by itself, and the exponent is the number of times the same base number has been multiplied. Power is defined as a base number raised to the exponent.
The power of two is called a square.
The square function's name derives from the fact that a square with sides of length \(l\) equals \(l^2\) has a significant role to play in the definition of area.
The area is inversely proportional to size: the area of a form that is \(n\) times larger is \(n^2\) times larger.
To learn more about powers, refer to the link below:
https://brainly.com/question/27307830
#SPJ4
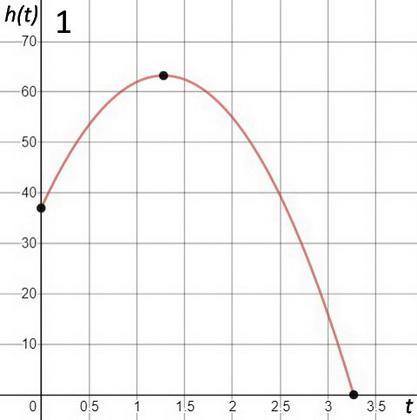
A water balloon is tossed vertically from a window at an initial height (s-sub zero) of 37 feet and with an initial velocity(v-subzero) of 41 feet per second. Answer the following using the fact that h(t)=-16T^2+v-sub zer0t+s sub zero. a) Determine a formula, h)t), for the function that models the height of the water balloon at time t . b)Plot the function in Desmos in an appropriate window. Use the graph to estimate the time the water balloon lands c)Use algebra to find the exact time the water balloon lands. Show your work. No decimals in your answer. d)Determine the exact time the water balloon reaches its highest point and its height at that time. e)4 pts] Compute the average rate of change of on the intervals . Include units on your answers and write a sentence to explain the meaning of the values you found. Arc{1.5,2}____________________________. Explanation: Arc{2,2.5}____________________________. Explanation: årc{2.5,3}____________________________. Explanation:
Answers
Answer:
a) h(t) = -16t^2 +41t +37
b) see attached (3.270 seconds)
c) (41+√4049)/32 seconds
d) 1.28125 seconds; 63.265625 feet
e) [1.5, 2]: -15; [2, 2.5]: -31; [2.5, 3]: -47
Step-by-step explanation:
a) The formula and initial values are given. Putting those values into the formula, we get ...
h(t) = -16t^2 +41t +37
__
b) The graph is attached. It shows the t-intercept to be about 3.270 seconds.
__
c) Using the quadratic formula, we can find the landing time as ...
\(t=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}=\dfrac{-41\pm\sqrt{41^2-4(-16)(37)}}{2(-16)}\\\\=\dfrac{41\pm\sqrt{4049}}{32}\qquad\text{only $t>0$ is useful}\)
The exact landing time is (41+√4049)/32 seconds.
__
d) The highest point is at t=-b/(2a) = -41/(2(-16)) = 41/32 seconds.
The value of the function at that point is ...
h(41/32) = (-16(41/32) +41)(41/32) +37 = 41^2/64 +37 = 4049/64
The maximum height is 4049/64 = 63.265625 feet.
__
e) For a quadratic function, that average rate of change on an interval is the derivative at the midpoint of the interval. Here, the derivative is ...
h'(t) = -32t +41 . . . in feet per second
Then the average rates of change are ...
arc[1.5, 2] = h'(1.75) = -32·1.75 +41 = -15 ft/s
arc[2, 2.5] = h'(2.25) = -32(2.25) +41 = -31 ft/s
arc[2.5, 3] = h'(2.75) = -32(2.75) +41 = -47 ft/s
These are the average velocity of the water balloon over the given interval(s) in ft/s. Negative indicates downward.

Answer:
(a) h(t) = -16t² + 41t + 37
(b) About 3.3 s
\(\large \boxed{\text{(c) }\dfrac{41+ \sqrt{4049}}{32}\text{ s}}\)
(d) -15 ft/s; -31 ft/s; -47 ft/s
Step-by-step explanation:
(a) The function
h(t) = -16t² + v₀t + s₀
v₀ = 41 ft·s⁻¹
s₀ = 37 ft
The function is
h(t) = -16t² + 41t + 37
(b) The graph
See Fig. 1.
It looks like the water balloon lands after about 3.3 s.
(c) Time of landing
h = -16t² + 41t + 37
a = -16; b = 41; c = 37
We can use the quadratic formula to solve the equation:
\(h = \dfrac{-b\pm\sqrt{b^2 - 4ac}}{2a} = \dfrac{-b\pm\sqrt{D}}{2a}\)
(i) Evaluate the discriminant D
D = b² - 4ac = 41² - 4(-16) × 37 = 1681 + 2368 = 4049
(ii) Solve for t
\(\begin{array}{rcl}h& = & \dfrac{-b\pm\sqrt{D}}{2a}\\\\ & = & \dfrac{-41\pm\sqrt{4049}}{2(-16)}\\\\ & = & \dfrac{41\pm\sqrt{4049}}{32}\\\\t = \dfrac{41- \sqrt{4049}}{32}&\qquad& t = \dfrac{41+ \sqrt{4049}}{32}\\\\\end{array}\\\)
\(\text{The water balloon will land after $\large \boxed{\mathbf{\dfrac{41+ \sqrt{4049}}{32}}\textbf{ s}} $}\)
(d) Time and maximum height
(i) Time
The axis of symmetry (time of maximum height) is at t = -b/(2a)
\(t = \dfrac{-41}{2(-16)} = \dfrac{41}{32} = \textbf{1.281 s}\)
(ii) Maximum height
The vertex is at y = h(1.281) = h(t) = -16(1.281)² + 41(1.281) + 37 = 63.27 ft
(e) Average rate of change
(i) Arc{1.5,2}
h(1.5) = 62.5
h(2) = 55
m = (h₂ - h₁)/(t₂ - t₁) = (55 - 62.5)/(2 - 1.5) = -7.5/0.5 = -15 ft/s
The water balloon has started to fall after it has reached peak height, so it is not going very fast
(ii) Arc{2,2.5}
h(2.5) =39.5
m = (39.5 - 55)/(2 - 1.5) = -15.5/0.5 = -31 ft/s
The balloon is in mid-fall, so gravity has caused it to speed up.
(iii) Arc{2.5,3}
h(3) = 16
m = (16 - 39.5)/(2 - 1.5) = -23.5/0.5 = -47 ft/s
The balloon is about to hit the ground, so it is falling at almost its maximum velocity.
Fig. 2 shows the height of the balloon at the above times.

anna enjoys dinner at a restaurant in washington, d.c., where the sales tax on meals is 10\%. she leaves a 15\% tip on the price of her meal before the sales tax is added, and the tax is calculated on the pre-tip amount. she spends a total of 27.5027.50 dollars for dinner. what is the cost of her dinner without tax or tip in dollars?
Answers
The cost of the dinner without tax or tip is $22.
Given,
The sales tax on meals = 10%
Tip she leaved before sales tax is added = 15%
The total amount for dinner = $27.50
We have to find the cost of dinner without adding tax or tip;
Let cost of meals be x.
Then,
She pays 10% of x as a sales tax
So that brings the total up to 100% + 10% = 110%
Before paying, she pays 15% on x as her tip. The tax does not touch the tip.
So that brings the total up to 100% + 10% + 15% = 125% of this is based on x, the cost of the meal.
So 125% of x = 27.50
125/100 * x = 27.50
125/100 * 100/125x = 100/125 * 27.50
x = 100/125 * 27.50
x = 2750 / 125 = 22
That is, the cost of the dinner without tax or tip is $22.
Learn more about cost of dinner here;
https://brainly.com/question/11862385
#SPJ4
Answer the following questions. "Proof by Venn diagram" is not an acceptable approach. Remember that mathematics is a language, and it is necessary to use correct grammar and notation. 1. If A and B are ANY two sets, determine the truth-values of the following statements. If a statement is false, give specific examples of sets A and B that serve as a counter- example (3 pts each). a. (A\B) CA b. Ac (AUB)
Answers
In this question, we are asked to determine the truth-values of two statements involving sets A and B. For each statement, we need to determine if it is true or false. If it is false, we need to provide specific counterexamples by choosing appropriate sets A and B.
a. (A\B) ⊆ A
The statement (A\B) ⊆ A is true for any sets A and B. This is because the set difference (A\B) contains elements that are in A but not in B. Therefore, by definition, every element in (A\B) is also an element of A. There are no counterexamples to this statement.
b. A^c ⊆ (AUB)
The statement\(A^c\) ⊆ (AUB) is true for any sets A and B. This is because the complement of A, denoted as \(A^c\), contains all elements that are not in A.
On the other hand, the union of A and B, denoted as (AUB), contains all elements that are in A or in B or in both.
Since the complement of A contains all elements not in A, it includes all elements in B that are not in A as well.
Therefore, \(A^c\) ⊆ (AUB) holds true for any sets A and B. There are no counterexamples to this statement.
In conclusion, both statements are true for any sets A and B, and there are no counterexamples.
To learn more about sets visit:
brainly.com/question/30705181
#SPJ11
Can someone help me its urgent

Answers
the surface area of the regular pyramid is approximately \(40sqrt(14) + 43.3 mm^2.\)To find the surface area of a regular pyramid, we need to find the area of each triangular face and add them together, then add the area of the base.
Let's start with finding the area of each triangular face. Since the pyramid is regular, all the triangular faces will be congruent, so we just need to find the area of one.
We know that the base of the triangle is 10 mm, and the height of the triangle is half the distance between the apex (the point at the top of the pyramid) and the base. Since the pyramid is regular, the apex is directly above the center of the base.
The height of the pyramid can be found using the Pythagorean theorem, where the height of the pyramid (h) is the hypotenuse of a right triangle with the base (b) and half the slant height (s) as the legs.
\(s^2 = hr^2 - (b/2)^2\)
We know the base is 10 mm and the height of the big triangle is 9 mm, so the half slant height is:
\(s = sqrt(h^2 - (b/2)^2) = sqrt(9^2 - (10/2)^2) = sqrt(81 - 25) = sqrt(56) = 2sqrt(14)\)
Now we can find the area of one triangular face using the formula:
Area = 1/2 x base x height
Area = 1/2 x 10 mm x 2sqrt(14) mm = \(10sqrt(14) mm^2\)
Since there are four triangular faces, the total area of the triangular faces is:
4 x 10sqrt(14) mm{power}2 = \(40sqrt(14) mm^2\)
Finally, we need to add the area of the base, which we know is 43.3 \(mm^2.\)
So the total surface area of the pyramid is:
\(Surface Area = 40sqrt(14) mm^2 + 43.3 mm^2 = 40sqrt(14) mm^2 + 43.3 mm^2 = 40sqrt(14) + 43.3 mm^2\)
Therefore, the surface area of the regular pyramid is approximately \(40sqrt(14) + 43.3 mm^2.\)
To know more about surface area of the regular pyramid click here:
brainly.com/question/27850123
#SPJ1
Prove that the points A (-3,-1), B(6,5) and C (3,3) are collineas
Answers
Answer:
nose porque está en una idioma que no se
Answer:
see explanation
Step-by-step explanation:
To show the points are collinear, that is lie on the same line.
Then the slope between A and B, B and C must be equal
Calculate slope m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = A(- 3, - 1) and (x₂, y₂ ) = B(6, 5)
\(m_{AB}\) = \(\frac{5+1}{6+3}\) = \(\frac{6}{9}\) = \(\frac{2}{3}\)
Repeat with (x₁, y₁ ) = B(6, 5) and (x₂, y₂ ) = C(3, 3)
\(m_{BC}\) = \(\frac{3-5}{3-6}\) = \(\frac{-2}{-3}\) = \(\frac{2}{3}\)
Since the slope between the 2 segments are equal and there is a common point B.
Then the points A, B and C are collinear
suppose that prior to conducting a coin-flipping experiment, we suspect that the coin is fair. how many times would we have to flip the coin in order to obtain a 99% confidence interval of width of at most .18 for the probability of flipping a head? (note that the z-score was rounded to three decimal places in the calculation) a) 164 b) 205 c) 167 d) 212 e) 202 f) none of the above
Answers
The coin is flipped at least 52 times in order to obtain a 99% confidence interval of width of at most . 18 for the probability of flipping a head.
Hence, Option F is correct answer.
In a sample with a number n of people surveyed with a probability of a success of π , and a confidence level of (1-α), we have the following confidence interval of proportions.
\(\pi\) ± z\(\sqrt{\frac{\pi \p(1-\pi )}{n} }\)
z is the z-score that has a pvalue of \(1-\frac{\alpha }{2}\)
Since, the coin is fair, so \(\pi =0.5\).
The margin of error is:
\(M=z\sqrt{(\frac{\pi (1-\pi )}{n} )}\)
99% confidence level:
So \(\alpha =0.01\) ,z is the value of Z that has a p value of 1-\(\frac{0.01}{2}\)=0.995,
so Z= 2.575
How many times would we have to flip the coin ?
We have to flip the coin in order to obtain a 99% confidence interval of width of at most 18 for the probability of flipping a head at least n times.
n is found when M=0.18 .
So
M=\(z\sqrt{\frac{\pi (1-\pi )}{n} }\)
\(0.18=2.575\sqrt{\frac{0.5*0.5}{n} }\)
\(0.18\sqrt{n} =2.575*0.5\)
\(\sqrt{n}=\frac{2.575*0.5}{0.18}\)
\(\sqrt{n} ^{2} =(\frac{2.575*0.5}{0.18} )^{2}\)
n = 51.16
Thus, we have to flip the coin at least 52 times.
Learn more about the Probability here: https://brainly.com/question/24756209
#SPJ4
Post 3 things you Notice or 3 things you Wonder about

Answers
Solve each equation. log 5x+1=-1
Answers
Answer:
\(5x = - 1 - 1 = 5x \div 5 = - 2 \div 5 = 2 \div 5\)