Find the outer perimeter.
10 ft
8 ft
P = [?] ft
Round to the nearest
hundredth.
![Find The Outer Perimeter.10 Ft8 FtP = [?] FtRound To The Nearesthundredth.](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/7EvHyencKRFpdGTt52k0dh04ctqGIN8m.png)
Answers
The outer perimeter is 76.12 ft according to given question.
what is perimeter?
Perimeter is a term used in geometry to refer to the total distance around the outside of a two-dimensional shape. It is the sum of the lengths of all the sides of the shape. For example, in a rectangle, the perimeter is calculated by adding the length of all four sides. In a circle, the perimeter is called the circumference and is calculated as the distance around the edge of the circle.
The perimeter of a semicircle is the sum of the length of its straight edge and half the circumference of the circle.
In this case, the radius of the semicircle is given as 8 units, so the circumference of the corresponding full circle is 2πr = 2π(8) = 16π units.
Half the circumference of the circle is therefore 8π units.
The straight edge of the semicircle is simply the diameter of the circle, which is twice the radius, or 2(8) = 16 units.
So, the perimeter of the semicircle is the sum of the straight edge and half the circumference:
Perimeter = 16 + 8π
Using approximate value for pi (π = 3.14), the perimeter can be expressed as:
Perimeter ≈ 16 + 8(3.14) ≈ 40.12 units.
The perimeter of a rectangle is given by the sum of the lengths of its four sides.
In this case, the length of the rectangle is given as 10 units and its width is given as 8 units.
Therefore, the perimeter of the rectangle is:
Perimeter = 2(Length + Width) = 2(10 + 8) = 2(18) = 36 units.
So, the perimeter of the rectangle with length 10 units and width 8 units is 36 units.
To know more about perimeter visit:-
https://brainly.com/question/397857
#SPJ1
Related Questions
Which segment represents a radius of the circle below?

Answers
Answer: Choose A my smart self just knew
First to answer gets brainliest
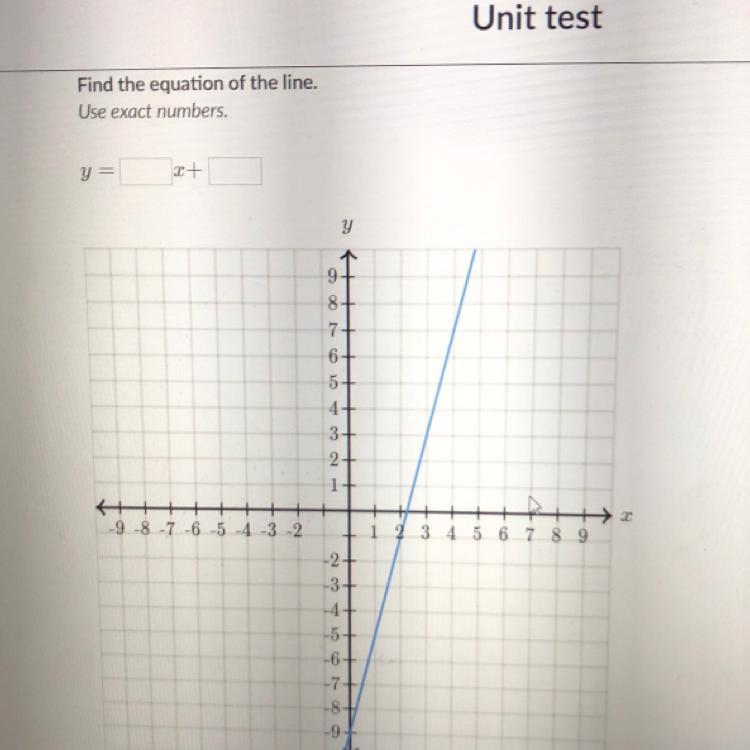
Answers
Answer:
y = 4x - 9
Step-by-step explanation:
Take 2 points:
(0,-9) and (4,7)
Find the slope:
(7 - (-9))/(4 - 0)
16/4 = 4
so we have y = 4x + b
Now find b:
Insert a point for y and x:
7 = 4(4) + b
7 = 16 + b
b = -9
y = 4x - 9
Circle O has a radius of 12.
Find the area of the shaded region rounded to the nearest whole number.

Answers
Answer:
~ 340
Step-by-step explanation:
A = pi * r^2
The big circle is r1 = 12cm so the small r2=6cm
A= A1 - A2 = (pi * r1^2)-( pi*r2^2) = 339,29 ~ 340 square cm
If the radius of the small circle is 12cm then: r1 = 24cm and r2 = 12cm and calculate it the same way
Jerarquía
de operaciones de números racionales (enteros, decimales y fraccionarios)
que son
Answers
Step-by-step explanation:
Los enteros son números enteros. Las fracciones son partes por elemento entero. Los decimales son fracciones expresadas en décimas.
What is 2.079404467 to 1 decimal place
Answers
Rounding 2.079404467 to 1 decimal place means keeping only one digit after the decimal point.
Looking at the second digit after the decimal point, which is 7, we see that it is greater than or equal to 5. Therefore, we round up the first digit after the decimal point, which is 9, by adding 1 to it.
So, rounding 2.079404467 to 1 decimal place, we get:
2.1
Therefore, 2.079404467 to 1 decimal place is equal to 2.1.
Answer this question correctly and you get brainliest

Answers
Answer:
3^2 x 7
Step-by-step explanation:
Multiply the polynomials.
(x + 2)(2x2 + 9x+8)
A. 2x3 + 13x2 – 26x+ 16
B. 16x3 + 72x2 + 46x - 16
C. 2x3 + 17x + 22x+16
D. 2x3 + 13x2 + 26x+ 16
Answers
Answer:
2x^3 + 13x^2 + 26x + 16
Step-by-step explanation:
x(2x^2 + 9x + 8) +2(2x^2 + 9x + 8)
2x^3 + 9x^2 + 8x + 4x^2 + 18x + 16
2x^3 + 13x^2 + 26x + 16
HOPE IT'S HELPFULRemoving which point from the coordinate plane would make the graph a function of x? On a coordinate plane, points are at (negative 2, negative 3), (negative 2, 1), (negative 4, 3), (0, 4), (1, 1), and (2, 3).
Answers
Answer: The first or the second point (- 2, - 3) or (- 2, 1)
Step-by-step explanation:
Ok, a relation (x, y) is a function only if, for each value x in the domain, we have only one value y in the range such that:
f(x) = y.
Here we have the pairs:
(- 2, - 3), (- 2, 1), (- 4, 3), (0, 4), (1, 1), and (2, 3).
Here, for the value x = -2, we have two different values of y.
y = 1 and y = 3.
So this is not a function, then if we want that this relation becomes a function, we must remove the first or the second point.
Answer:
I think B
Step-by-step explanation:
Divide 49 m²by Square root 7 m
Answers
Step-by-step explanation:
Here is your answer in the attachment
Hope it helps you
LCM of 18 and 22 = ?
Answers
Answer:
198
Step-by-step explanation:
Make use of the multiples that can divide both of them until their remainders are both 1

The population for a clinical study has 500 Asian, 1000 Hispanic and 500 Native American people. What is good way of sampling this population to ensure that the distribution of various sub-populations is maintained if only 200 samples have to be chosen? Give the distribution of the various sub-populations in the final sample.
Answers
A good way to sample this population while maintaining the distribution of various sub-populations is by using stratified sampling. In stratified sampling, the population is divided into homogeneous subgroups or strata based on certain characteristics, and then a random sample is selected from each stratum.
To ensure that the distribution of various sub-populations is maintained, the sample should include a proportional representation of individuals from each subgroup. In this case, the subgroups are Asian, Hispanic, and Native American.
Here's how the distribution of the various sub-populations can be maintained in the final sample:
1. Determine the proportion of each subgroup in the population:
- Asian: 500 / 2000 = 0.25 (25%)
- Hispanic: 1000 / 2000 = 0.5 (50%)
- Native American: 500 / 2000 = 0.25 (25%)
2. Calculate the number of samples to be chosen from each subgroup:
- Asian: 0.25 * 200 = 50 samples
- Hispanic: 0.5 * 200 = 100 samples
- Native American: 0.25 * 200 = 50 samples
3. Randomly select the specified number of samples from each subgroup.
By using stratified sampling with the specified proportions, the final sample of 200 individuals will have a distribution that reflects the proportions of Asian, Hispanic, and Native American subpopulations in the overall population.
To know more about populations visit-
brainly.com/question/28426501
#SPJ11
* this problem requires the use of rstudio * you collected data from a random sample of 1000 movies from the moviedb.org. you saved the data frame as 1000movies in rstudio. the data frame is in the rdata file sent over email. build a multiple linear regression model that predicts revenue-m based on budget m and genre2 the model will also include an interaction term between budget m and genre2 what is the intercept of the linear regression model? round the intercept to three decimal places.
Answers
The intercept of the linear regression model rounded to three decimal places is -29.678.
First, open the RData file in RStudio. Then, load the 1000movies data frame into the environment. Now, we can build the multiple linear regression model. We can do this using the lm() function in R. The lm() function takes a formula as the first argument.
The formula for our model will look like this:
revenue-m ~ budget-m + genre2 + budget-m:genre2.
This formula specifies that we want to use budget-m, genre2, and the interaction between budget-m and genre2 as predictor variables to predict revenue-m.
Next, we can fit the model using the lm() function. We can use the summary() function to view the results of the model. The intercept of the linear regression model is the value of revenue-m when budget-m and genre2 are both equal to 0.
In our model, the intercept is -29.678. Rounded to three decimal places, the intercept is -29.678.
For more questions like Linear regression model click the link below:
https://brainly.com/question/29447886
#SPJ4
Provide the Laplace transform for each of the functions below: h(t)=3te−2t→ g(t)=61sin(3t)→ f(t)=te−2t→
Answers
The answer of the given question based on the function is , the Laplace transform of h(t) is 3/s². , the Laplace transform of g(t) is 18/(s² + 9). , the Laplace transform of f(t) is 1/(s+2)².
Laplace transform for h(t)
The Laplace transform for h(t) = 3te^{-2t} can be calculated as follows:
L{h(t)} = ∫_0°° 3te^{-st} dt
= 3 ∫_0°° t e^{-st} dt
Applying integration by parts, we get:
L{h(t)} = 3[-t e^{-st}/s + (1/s) ∫_0°° e^{-st} dt]
= 3[-t e^{-st}/s + (1/s) * (-1/s) * e^{-st}]_0°°
= 3[0 + (1/s²)]
= 3/s²
Therefore, the Laplace transform of h(t) is 3/s².
Laplace transform for g(t)
The Laplace transform for g(t) = (6/1)sin(3t) can be calculated as follows:
L{g(t)} = ∫_0°° (6/1) sin(3t) e^{-st} dt
= (6/1) ∫_0°° sin(3t) e^{-st} dt
The Laplace transform of sin(at) is given by:
L{sin(at)} = a/(s² + a²)
Therefore, L{g(t)} = (6/1) * 3/(s² + 3²)
= 18/(s² + 9)
Therefore, the Laplace transform of g(t) is 18/(s² + 9).
Laplace transform for f(t)
The Laplace transform for f(t) = te^{-2t} can be calculated as follows:
L{f(t)} = ∫_0°° te^{-2t} e^{-st} dt
= ∫_0°° t e^{-(s+2)t} dt
Applying integration by parts, we get:
L{f(t)} = [-t e^{-(s+2)t}/(s+2) + (1/(s+2)) ∫_0°° e^{-(s+2)t} dt]
= [-t e^{-(s+2)t}/(s+2) + (1/(s+2)) * (-1/(s+2)) * e^{-(s+2)t}]_0°°
= [0 + (1/(s+2)²)]
= 1/(s+2)²
Therefore, the Laplace transform of f(t) is 1/(s+2)².
To know more about Integration visit:
https://brainly.in/question/9972223
#SPJ11
The Laplace transform of each of the functions below is as follows:h(t)= 3te^-2t → H(s) = 3/(s+2)^2g(t)= 6/1 sin(3t) → G(s) = 18/(s^2 + 9)f(t)= te^-2t → F(s) = 1/(s+2)^2Where L stands for the Laplace transform operator.
Laplace transform:
L{f(t)} = F(s) = ∫f(t) e^-st dt
Where "s" is the complex frequency parameter and t is time.
Laplace transform of h(t) = 3t e^-2t We are going to apply integration by parts to solve it.
We choose u=t, and dv = e^-2t dt.
Then we have du = dt and v = -1/2 e^-2t.
Now applying the formula for integration by parts,
we getH(s) = L{h(t)} = ∫ 0∞ 3t e^-st dt = [3(-1/2)te^-2t - ∫-1/2 e^-2t dt] = [-3/2 te^-2t + 3/4 e^-2t]_0∞ = 3/(s+2)^2
Laplace transform of g(t) = 6/1 sin(3t)
We know that the Laplace transform of sin(at) is a/ (s^2 + a^2)
Hence,G(s) = L{g(t)} = 6/1 [3/(s^2 + 3^2)] = 18/(s^2 + 9) Laplace transform of f(t) = t e^-2t
We know that the Laplace transform of t^n is n!/s^(n+1)
Hence,F(s) = L{f(t)} = 1/ (s+2)^2
To know more about , function visit:
https://brainly.com/question/11624077
#SPJ11
A wave has a period of \( 0.5 \mathrm{~s} \) and a wavelength of \( 13 \mathrm{~cm} \). What is the velocity of the wave?
Answers
The wave has a velocity of 26 cm/s.
We have the wave's period and wavelength.
The velocity of the wave can be determined using the formula for wave velocity, which is:
\(\[v = \frac{\lambda}{T}\]\)
The period of a wave is the time it takes for one complete wave to pass through a point. The wavelength of a wave is the distance between two successive points on the wave that are in phase with one another.
To determine the velocity of a wave, we can use the formula v = λ/T, where v is the wave's velocity, λ is its wavelength, and T is its period.
In this particular case, the wave has a period of 0.5 s and a wavelength of 13 cm. To calculate the velocity, we simply substitute these values into the formula:
v = λ/T = 13 cm/0.5 s = 26 cm/s Therefore, the velocity of the wave is 26 cm/s.
To know more about points visit:
brainly.com/question/30891638
#SPJ11
PLSSSS HELP IF YOU TURLY KNOW THISSS

Answers
Answer:
7
Step-by-step explanation:
To find the value of x, we need to subtract 7 on both sides.
Subtract 7 from 7 to get 0. This cancels itself out, and isolates the x.
Then, subtract 7 from 14 to get 7.
This leaves us with the equation x =7.
Answer:
\( \sf \: x = 7\)
Step-by-step explanation:
Now we have to,
→ Find the required value of x.
The equation is,
→ x + 7 = 14
Then the value of x will be,
→ x + 7 = 14
→ x = 14 - 7
→ [ x = 7 ]
Hence, the value of x is 7.
The heights of a certain breed of dogs has a normal distribution with a mean of 28 inches and a standard deviation of 4 inches. If we randomly select 64 of these dogs, what is the probability that the mean height of 64 dogs is: a) Less than 27 inches? b) Greater than 28.5 inches? c) Between 27 and 28.5 inches?
Answers
The probability that the mean height of 64 dogs is between 27 and 28.5 inches is approximately 0.8531.
We can use the central limit theorem to approximate the distribution of the sample mean. The central limit theorem states that if we take a large enough sample from a population, the sample mean will be approximately normally distributed with mean equal to the population mean and standard deviation equal to the population standard deviation divided by the square root of the sample size. In this case, we have:
Population mean (μ) = 28 inches
Population standard deviation (σ) = 4 inches
Sample size (n) = 64
a) To find the probability that the mean height of 64 dogs is less than 27 inches, we need to standardize the sample mean and find the corresponding area under the standard normal distribution. We have:
z = (sample mean - population mean) / (population standard deviation / sqrt(sample size))
z = (27 - 28) / (4 / sqrt(64))
z = -2
Using a standard normal distribution table or calculator, we find that the probability of z being less than -2 is approximately 0.0228. Therefore, the probability that the mean height of 64 dogs is less than 27 inches is approximately 0.0228.
b) To find the probability that the mean height of 64 dogs is greater than 28.5 inches, we standardize the sample mean and find the area to the right of the standardized value. We have:
z = (sample mean - population mean) / (population standard deviation / sqrt(sample size))
z = (28.5 - 28) / (4 / sqrt(64))
z = 1
Using a standard normal distribution table or calculator, we find that the probability of z being greater than 1 is approximately 0.1587. Therefore, the probability that the mean height of 64 dogs is greater than 28.5 inches is approximately 0.1587.
c) To find the probability that the mean height of 64 dogs is between 27 and 28.5 inches, we need to find the area under the standard normal distribution between the two standardized values. We have:
z1 = (27 - 28) / (4 / sqrt(64))
z1 = -2
z2 = (28.5 - 28) / (4 / sqrt(64))
z2 = 1
Using a standard normal distribution table or calculator, we find that the probability of z being between -2 and 1 is approximately 0.8531. Therefore, the probability that the mean height of 64 dogs is between 27 and 28.5 inches is approximately 0.8531.
For such more questions on probability
https://brainly.com/question/24756209
#SPJ11
Kim has health insurance with a deductible of $500 and an 80/20 coinsurance. How much will she pay if she incurs a loss of $1,500?
a.$200
b.$500
c.$700
d.$1,300
Answers
If Kim has health insurance with a deductible of $500 and 80/20 coinsurance then amount she pay if she incurs a loss of $1500 is (c)$700 .
In an 80/20 coinsurance, the insurance company pays 80% of covered expenses after the deductible has been met, and the policyholder is responsible for paying the remaining 20%.
So , if Kim incurs a loss of $1500, she first needs to pay the $500 deductible before her insurance kicks in. After that, she will pay for 20% of the remaining $1000 in covered expenses:
⇒ 20% of $1,000 = $200
So, in total, Kim will pay $500 for the deductible plus $200 in coinsurance, for a total of:
⇒ $500 + $200 = $700
Therefore, If Kim will pay (c) $700.
Learn more about Coinsurance here
https://brainly.com/question/28463232
#SPJ4
there are 200 students in cs6515, 140 are cs master students, 50 are cs phd students, and 30 are from other departments. if one choses a student at random until a cs phd student is selected, what is the expected number of choices needed?
Answers
The expected number of choices needed to select the first CS PhD student is 4.
To solve this problem, we can use the concept of geometric distribution. The geometric distribution represents the number of independent and identical trials that are needed to obtain the first success, where the probability of success is p.
In this case, the probability of selecting a CS PhD student on any given trial is 50/200 = 0.25. Therefore, the number of trials needed to obtain the first CS PhD student follows a geometric distribution with p = 0.25.
The expected value of a geometric distribution with parameter p is given by E(X) = 1/p. Therefore, the expected number of choices needed to select the first CS PhD student is
E(X) = 1/p = 1/0.25 = 4
Learn more about geometric distribution here
brainly.com/question/29210110
#SPJ4
2017b "Courage is not the absence of fear, but rather the judgment that something else is more important than one's fear."
—Ambrose Hollingworth Redmoon
Choose a work of fiction in which a character makes a judgment
that "something else" is more important than fear. Then, in a well-written essay, analyze how the complexity of that judgment reveals the character's dreams, goals, or values and contributes to an interpretation of the work as a whole.
Answers
Her journey highlights the importance of individual agency and the pursuit of justice in a world that is often cruel and unforgiving.
In George R.R. Martin's A Song of Ice and Fire series, Arya Stark is a character who repeatedly demonstrates the courage to act despite her fear. In particular, her decision to leave her family and pursue her own goals reveals the complexity of her judgment and her strong values of independence and justice.
Throughout the series, Arya experiences numerous traumatic events that could have easily left her paralyzed with fear. However, she consistently chooses to confront her fears head-on and take action in pursuit of her goals. For example, when her father is executed in front of her, Arya does not simply run away or hide. Instead, she watches and learns from the experience, using it as motivation to become stronger and seek revenge against those who have wronged her family.
One of the most significant moments in Arya's character arc is when she decides to leave her family and begin training as an assassin. Despite her love for her family, Arya realizes that she will never be able to achieve her goals of justice and revenge by staying with them. Her decision to leave shows a deep understanding of her values and priorities, and a willingness to put those things ahead of her own fears and desires.
Furthermore, Arya's journey to becoming an assassin reveals the complexity of her judgment. She does not simply blindly follow orders or embrace the violent culture of the Faceless Men. Instead, she learns to use her skills for her own purposes, such as avenging her family and protecting the innocent. Her commitment to justice and independence is a driving force behind her decisions and actions.
Overall, Arya's courage in the face of fear is a key aspect of her character and contributes to a larger interpretation of the series. Her decision to leave her family and pursue her own goals shows a complex judgment that reflects her values and priorities. Through her actions, Arya embodies the idea that courage is not simply the absence of fear, but rather a willingness to prioritize something else above that fear. Her journey highlights the importance of individual agency and the pursuit of justice in a world that is often cruel and unforgiving.
To learn more about George R.R. Martin's visit:https://brainly.com/question/8908874
#SPJ11
⎧
21x+7y=42
−5x+5y=10
Answers
Answer:
(1, 6.71)
Step-by-step explanation:
I'm assuming that you need to solve this by substitution or elimination since you didn't include any context in your question, just the equations.
To solve this by elimination, first, decide on a variable you want to get rid of / cancel out. I chose y. To do this, you need to find the least common multiple (LCM) of 7 and 5, which is 35. Now, multiply the top equation, 21x + 7y = 42, by -5. Multiply the bottom equation, -5x + 5y = 10, by 7. Make sure when you multiply that you either make the 5 or the 7 negative so you can cancel out y. I chose to make 5 negative.
After you multiply by the -5 and the 7, rewrite your new equations:
-105x - 35y = -210
-35x + 35y = 70
Now, add the two equations together. When you do this, the y's cancel out and you're left with -140x = -140. Now, divide both sides by -140, and you're left with x = 1. Plug the value of x into one of your original equations. I chose the bottom equation, -5x + 5y = 10.
-5(1) + 7y = 42 -----> -5 + 7y = 42.
Add -5 to both sides, which gives you 7y = 47. Divide both sides by 7, which gives you y = 6.71.
The last step is to put the values of x and y into a point: (1, 6.71).
Hope this helps!
which expression is equivalent to 1/sin(2x) - cos(2x)/sin(2x)
Answers
Answer:recall your product-to-sum formulas, with
a = 2x
and
b = x
Now apply the formula for sina cosb
or, you can make it 2sinx cosx cosx and massage that to get one of your choices
Step-by-step explanation:
Answer:
A. Tan(x)
Step-by-step explanation:
Edge 2020
Can someone please look at my script and explain why the data is not being read and entered into my pretty table? Any help is appreciated. Script is below. I am getting an empty pretty table as my output.
# Python Standard Library
import os
from prettytable import PrettyTable
myTable = PrettyTable(["Path", "File Size", "Ext", "Format", "Width", "Height", "Type"])
dirPath = input("Provide Directory to Scan:") i
f os.path.isdir(dirPath):
fileList = os.listdir(dirPath)
for eachFile in fileList:
try:
localPath = os.path.join(dirPath, eachFile)
absPath = os.path.abspath(localPath)
ext = os.path.splitext(absPath)[1]
filesizeValue = os.path.getsize(absPath)
fileSize = '{:,}'.format(filesizeValue)
except:
continue
# 3rd Party Modules from PIL
import Image imageFile = input("Image to Process: ")
try:
with Image.open(absPath) as im: #
if success, get the details imStatus = 'YES'
imFormat = im.format
imType = im.mode
imWidth = im.size[0]
imHeight = im.size[1]
#print("Image Format: ", im.format)
#print("Image Type: ", im.mode)
#print("Image Width: ", im.width)
#print("Image Height: ", im.height)
except Exception as err:
print("Exception: ", str(err))
myTable.add_row([localPath, fileSize, ext, imFormat, imWidth, imHeight, imType])
print(myTable.get_string())
Answers
The data is not being read file and entered into the pretty table because there is a name error, `imFormat`, `imType`, `imWidth`, and `imHeight` are not declared in all cases before their usage. Here is the modified version of the script with corrections:```
# Python Standard Library
import os
from prettytable import PrettyTable
from PIL import Image
myTable = PrettyTable(["Path", "File Size", "Ext", "Format", "Width", "Height", "Type"])
dirPath = input("Provide Directory to Scan:")
if os.path.isdir(dirPath):
fileList = os.listdir(dirPath)
for eachFile in fileList:
try:
localPath = os.path.join(dirPath, eachFile)
absPath = os.path.abspath(localPath)
ext = os.path.splitext(absPath)[1]
filesizeValue = os.path.getsize(absPath)
fileSize = '{:,}'.format(filesizeValue)
except:
continue
# 3rd Party Modules from PIL
imageFile = input("Image to Process: ")
try:
with Image.open(absPath) as im:
# If successful, get the details
imStatus = 'YES'
imFormat = im.format
imType = im.mode
imWidth = im.size[0]
imHeight = im.size[1]
except Exception as err:
print("Exception: ", str(err))
continue
myTable.add_row([localPath, fileSize, ext, imFormat, imWidth, imHeight, imType])
print(myTable)
```The above script now reads all the images in a directory and outputs details like format, width, and height in a pretty table.
To know more about read a file refer here :
https://brainly.com/question/31670046#
#SPJ11
Hi I really need help with answering this! I will give you brainest! And is it okay if you explain why and how you got this answer, thanks so much!

Answers
Answer:
18 students took the bus to school.
Step-by-step explanation:
If 1/4 of the students walked, that leaves 3/4 of the students who did not walk. That leaves 22.5 students. Out of these students 22.5, 4/5 of them take the bus, and 4/5 of 22.5 is 18.
Which of the binomials below is a factor of this trinomial? 4x2 + 12x + 9
A. 2x-3
B. 2x-1
C. 2x+1
D. 2x+3
Answers
Answer:
d-2x-3
Step-by-step explanation:
The factor of the trinomial will be (2x + 3) and (2x + 3). Then the correct option is D.
What is a factorization?It is a method for dividing a polynomial into pieces that will be multiplied together. At this moment, the polynomial's value will be zero.
The trinomial is given below.
⇒ 4x² + 12x + 9
Then the factor of the trinomial will be
⇒ 4x² + 12x + 9
⇒ 4x² + 6x + 6x + 9
⇒ 2x(2x + 3) + 3(2x + 3)
⇒ (2x + 3)(2x + 3)
⇒ (2x + 3)²
Then the correct option is D.
More about the factorization link is given below.
https://brainly.com/question/6810544
#SPJ2
Ferris wheel in London; England It stands 135 meters tall with a The London Eye iS a giant diamederof 120 meters: It takes half an hour to complete one revolution form hlt) = A cos( Br D t0 model the height; h (in meters). Find cosine funclion of the (in minutes). Assume the passenger passenger riding the London Eye as a function of time 0. Sketch the graph of one period on the next page and is at the bottom of the wheel at time use it to help you answer the following questions and create your function What is a rider' height at m = 0 minutes? (Hint: It is not 0 meters) 2. How long does it take for a rider to reach the top? What is the rider's height at that time? What is the period of this function? Use the period to find What is the vertical shift and amplitude of this function? 5 . Find The Equation Of Your Cosine Function, Use your function to find a rider's height at =21minutes. Sketch the graph ofyour function (This helps to answer the previous questions)
Answers
The height of a rider on the London Eye Ferris wheel in London can be modeled by the function h(t) = A * cos(B * t), where t represents time in minutes. The Ferris wheel stands 135 meters tall with a diameter of 120 meters. It takes half an hour (30 minutes) to complete one revolution.
1. At t = 0 minutes, the rider is not at the bottom of the wheel but at the midpoint of the wheel's diameter, so the rider's height is equal to the radius of the wheel, which is half of its diameter. Therefore, the rider's height at t = 0 minutes is 120/2 = 60 meters.
2. To determine the time it takes for the rider to reach the top, we need to find the period of the cosine function. The period (T) is the time it takes for one complete cycle of the function. In this case, the period is equal to the time it takes for the Ferris wheel to make a full revolution, which is 30 minutes. So, the rider reaches the top after half of the period, which is T/2 = 30/2 = 15 minutes. At that time, the rider's height is equal to the sum of the radius of the wheel and its height, which is 60 + 135 = 195 meters.
3. The period of the cosine function is T = 30 minutes.
4. The vertical shift of the function represents the average height of the rider throughout one complete cycle. In this case, the average height is the sum of the radius and the height of the Ferris wheel divided by 2, which is (60 + 135)/2 = 97.5 meters. Therefore, the vertical shift of the function is 97.5 meters. The amplitude of the function is half of the vertical distance between the maximum and minimum values, which is (135 - 60)/2 = 37.5 meters.
5. The equation of the cosine function is h(t) = 97.5 + 37.5 * cos((2π/30) * t). To find the rider's height at t = 21 minutes, we substitute t = 21 into the equation: h(21) = 97.5 + 37.5 * cos((2π/30) * 21) ≈ 185.11 meters.
In summary, the rider's height at t = 0 minutes is 60 meters. It takes 15 minutes for the rider to reach the top, at which point their height is 195 meters. The period of the function is 30 minutes. The vertical shift is 97.5 meters, and the amplitude is 37.5 meters. Using the cosine function, the rider's height at t = 21 minutes is approximately 185.11 meters.
Learn more about cosine function here: brainly.com/question/3876065
#SPJ11
Two ways you can solve the following equation : 20 = 5(-3+x)
Answers
Answer:
x=7
Step-by-step explanation:
Answer:
Step-by-step explanation:
Method one:
You divide both sides by 5 and get
4= -3+x
7=x
Method 2:
You can distribute the 5
20= -15+5x
35=5x
x=7
Hi! can anyone help me? Question is down in the picture below! 10 points! Thank you!

Answers
Answer:2
Step-by-step explanation:
I’m not exactly sure bc I’ve never heard a problem like that before but I believe that’s correct.
Differentiate the function. z(y) = A/y¹³+ Beʸ
Answers
The derivative of the function z(y) = A/y¹³+ Beʸ is z'(y) = [-13A y¹² Beʸ] / [(y¹³ + Beʸ)²].
To differentiate the function z(y) = A/y¹³+ Beʸ, we'll use the quotient rule.
The quotient rule is a derivative rule that is used to differentiate two functions that are divided by each other.
It states that the derivative of a function f(x)/g(x) is [g(x)f'(x) - f(x)g'(x)] / [g(x)]².
How to differentiate the function z(y) = A/y¹³+ Beʸ:
To apply the quotient rule, let f(y) = A and g(y) = y¹³ + Beʸ.
Then, f'(y) = 0 and g'(y) = 13y¹² + Beʸ.
Using the quotient rule, the derivative of z(y) is given by:z'(y) = [g(y)f'(y) - f(y)g'(y)] / [g(y)]²= [(y¹³ + Beʸ)(0) - A(13y¹² + Beʸ)] / [(y¹³ + Beʸ)²]= [-13A y¹² Beʸ] / [(y¹³ + Beʸ)²]
Therefore, the derivative of the function z(y) = A/y¹³+ Beʸ is z'(y) = [-13A y¹² Beʸ] / [(y¹³ + Beʸ)²].
To know more about derivative, visit:
https://brainly.com/question/29144258
#SPJ11
Elliot make and ell key chain. Hi profit depend on what price he charge for a key chain. He write the expreion (x−10)(60−3x) to repreent hi profit baed on the price per key chain, x
Answers
The expression (x - 10)(60 - 3x) represents Elliot's profit based on the price per key chain, where x is the price in dollars that Elliot charges for each key chain.
The expression can be interpreted as follows:
x - 10 represents the revenue Elliot makes from each key chain, as it's equal to the price per key chain minus the cost of materials for each key chain.
60 - 3x represents the number of key chains Elliot can make and sell, as it's equal to the maximum amount of money Elliot has minus the total cost of materials for all key chains.
So, (x - 10)(60 - 3x) represents Elliot's total profit, which is equal to the revenue from each key chain multiplied by the number of key chains Elliot can make and sell.
In other words, Elliot's profit is proportional to both the price he charges per key chain and the number of key chains he can sell at that price. The expression captures this relationship and can be used to determine Elliot's profit for different prices.
To learn more about Profits
Visit; brainly.com/question/15190155
#SPJ4
The expression (x - 10)(60 - 3x) represents Elliot's profit based on the price per key chain, where x is the price in dollars that Elliot charges for each key chain.
The expression can be interpreted as follows:
x - 10 represents the revenue Elliot makes from each key chain, as it's equal to the price per key chain minus the cost of materials for each key chain.
60 - 3x represents the number of key chains Elliot can make and sell, as it's equal to the maximum amount of money Elliot has minus the total cost of materials for all key chains.
So, (x - 10)(60 - 3x) represents Elliot's total profit, which is equal to the revenue from each key chain multiplied by the number of key chains Elliot can make and sell.
In other words, Elliot's profit is proportional to both the price he charges per key chain and the number of key chains he can sell at that price. The expression captures this relationship and can be used to determine Elliot's profit for different prices.
To learn more about Profits Visit;
brainly.com/question/15190155
#SPJ4
10
00
8
6
4
2
-10-8-6
44
-22
24
6 8 10 X
What is the solution to the system of equations?
(-2 -8)
(-1 -5)
(0-2)
(24)
Answers
Answer:
not sure explain it better please