Answers
Answer:
the answer to your question is
2n + 20
Answer:
2n + 20
This is how it is written.
Related Questions
3b • a2
This for test
Answers
Basil was shown this enlargement, and he was asked to find the perimeter of the enlarged shape. His work is shown below.
A shape has side lengths 2, 2, 6, 4, 6. A larger shape has corresponding sides, A, A, 24, B, 24.
Figures not drawn to scale.
Basil’s Work
Scale factor
StartFraction 24 over 6 EndFraction = 4
Side A
4 times 2 = 8
Side B
4 times 4 = 16
Perimeter
24 + 16 + 8 + 8 = 56
Where, if any, did Basil first make a mistake in his work?
Answers
The answer to the mistake that Basil made in his enlargement work is; No, he did not make any mistake finding the perimeter.
How to interpret Shape Enlargement?From Basil's work we can see that Perimeter is gotten as;
24 + 16 + 8 + 8 = 56
Now, when we look at the newly enlarged shape lengths, we can see that the corresponding lengths are very correct and as such the perimeter is accurate and doesn't require any correction.
Read more about Shape Enlargement at; https://brainly.com/question/3457976
#SPJ1
A Ferris wheel can accommodate 60 people in 20 minutes. How many people could ride the Ferris wheel in 6 hours?
people in 6 hours
What was the rate per hour?
people per hour
Answers
Answer: 180 per hour, 1080 per 6 hours
Step-by-step explanation:
7. |-7) - 131 =
a. - 4
b. 4
C. 10
d. - 10
Answers
Answer:
Step-by-step explanation:
If the question is - 7 - 131 = - 138
arccsc(\(\frac{2}{3}\)\(\sqrt{3}\))
Answers
The arc cossecant of the given value is of 30º.
Cosecant and arc cosecantThe cosecant of an angle is given by the ratio between 1 and the sine of the angle, as follows:
cos(x) = 1/sin(x)
The arc cossecant of an angle is represented by the expression arc csc(x), and represents the inverse of the cossecant, that is, it is the angle which has a cosecant of x.
In this problem, the arc cossecant that is asked is:
\(\arccsc{\left(\frac{2}{3\sqrt{3}}\right)}\)
Basically, it asks for the angle which has a cossecant value of 2/(3sqrt(3)). This angle is found using a calculator, and it is of 30º.
Hence the numeric value of the expression is presented as follows:
\(\arccsc{\left(\frac{2}{3\sqrt{3}}\right)} = 30^\circ\)
More can be learned about cossecant and arc cossecant at https://brainly.com/question/13276558
#SPJ1
jason drove for three hours at an average speed of 55 miles per hour how far did he go?
Answers
Answer: 165 miles
Step-by-step explanation: In order to figure out the answer, you must do 55 x 3 because he drove for 3 hours at 55 mph so you could break it up and go 50 x 3 to equal 150 and 5 x 3 to equal 15 and add those to get 165.
Answer:
The answer is 165miles
Step-by-step explanation:
\(distance = speed \times time\)
d=55×3
d=165 miles
The solution set for -18 < 5x - 3 is _____.
3 > x
3 < x
-3 < x
-3 > x
Answers
Answer:
\(-3 < x\)
Step-by-step explanation:
Given
\(-18 < 5x-3\)
Required
The solution
\(-18 < 5x-3\)
Add 3 to both sides
\(3-18 < 5x-3+3\)
\(-15 < 5x\)
Divide both sides by 5
\(-3 < x\)
A roller coaster begins at 90.5 feet above ground level. Then it descends 105.25 feet. Find the height of the coaster after the first descent.
Answers
Answer:
14.75 feet below ground level.
Step-by-step explanation:
90.5-105.25=-14.75
Which is a shrink of an exponential growth function?
f(x) = One-third(3)x
f(x) = 3(3)x
f(x) = One-third (one-third) Superscript x
f(x) = 3 (one-third) Superscript x
Answers
Answer:
3 zero
Step-by-step explanation:
Answer:
The correct answer is A
Step-by-step explanation:
Hope This Helps
Mariel says that a jewelry box that is 3 inches high, 4 1/2 inches wide, and 5 inches long has a volume of 67 1/2 inches. Katie says that answer is not quite correct. What is the error in Mariel's answer?
Answers
Answer: inside width, length and heights may be smaller
Step-by-step explanation. Walls of box have certain thickness, assume 0.1 inches. Then inner measures would be 2.8 in, 4.3 in and 4.8 in. You need to reduce thickness of wall from both sides.
Mitch made a dot plot of the number of hours that students in his grade spent this week watching television. Use the data to choose true or false for each statement

Answers
Answer:
the first one is false
second one is True
Third one is false
fourth one is false
Step-by-step explanation:
I just looked at the chart please mark me brainlest answer
Answer:
the first one is false
second one is True
Third one is false
fourth one is false
Step-by-step explanation:
its right on envisions.
The formula for an account that earns
compound interest is Pt = P0 ⋅ (1 + r)
t
,
where Pt
represents the balance in the
account after t years, P0 represents the
initial amount of the deposit, and r
represents the interest rate.
Carrie is considering depositing $1480 into
an account that pays compound interest.
How much will be in her account if she
receives 1.9% compound interest for
10 years? Round to the nearest cent.
Answers
After 10 years with a Compound interest rate of 1.9%, the amount in Carrie's account will be approximately $1777.87.
The amount that will be in Carrie's account after 10 years with compound interest, we can use the formula Pt = P0 ⋅ (1 + r)^t.
Given:
P0 = $1480 (initial deposit)
r = 1.9% = 0.019 (interest rate as a decimal)
t = 10 (number of years)
Substituting these values into the formula, we get:
Pt = $1480 ⋅ (1 + 0.019)^10
Using a calculator, we can evaluate the expression inside the parentheses:
(1 + 0.019)^10 ≈ 1.201223
Now we can calculate the final amount in Carrie's account:
Pt ≈ $1480 ⋅ 1.201223
Pt ≈ $1777.87
Therefore, after 10 years with a compound interest rate of 1.9%, the amount in Carrie's account will be approximately $1777.87.
To know more about Compound interest rate.
https://brainly.com/question/3989769
#SPJ11
I am confused, can anybody help?

Answers
c^2 = a^2 + b^2
25^2 = 20^ 2 + b^2
625 = 400 + b^2
b^2 = 225
b = 15
X = 15
Use the limit definition of the derivative to find the slope of the tangent line to the curve f(x) = 7x ^ 2 + 2x + 3 at x = 1
Answers
Answer:
16
Step-by-step explanation:
Step 1: Write down the function \(f(x)=7x^2+2x+3.\)
Step 2: Write down the limit definition of the derivative:
\(f'(x)= lim_{h0} \frac{f(x+h)=f(x)}{h} .\)
Step 3: Substitute the function \(f(x)\) into the limit definition:
\(f'(x)=lim_{h0} \frac{(7(x+h)^2+2(x+h)+3)-(7x^2+2x+3)}{h}.\)
Step 4: Simplify the expression inside the limit:
\(f'(x)=lim_{h0}\frac{7x^2+14xh+7h^2+2x+2h+3-7x^2-2x-3}{h} .\)
Step 5: Combine like terms:
\(f'(x)=lim_{h0} \frac{14xh+7h^2+2h}{h} .\)
Step 6: Factor out an \(h\) from the numerator:
\(f'(x)=lim_{h0} \frac{h(14x+7h+2h}{h} .\)
Step 7: Cancel out the \(h\) in the numerator and denominator:
\(f'(x)=lim_{h0}(14x+7h+2).\)
Step 8: Evaluate the limit as \(h\) approaches 0:
\(f'(x)=14x+2.\)
Step 9: Substitute \(x=1\) into the derivative:
\(f'(1)=14(1)+2=14+2=16.\)
The Slope of the tangent line to the curve \(f(x)=7x^2+2x+3\) at \(x=1\) would be \(16.\)
Sketch the graph of each functiony=5+ √x
Answers
Given the function:
\(y=5+\sqrt[]{x}\)To sketch the graph, we calculate some points:
For ease of calculation, pick values of x that are perfect squares.
\(\begin{gathered} \text{When x=0} \\ y=5+\sqrt[]{0} \\ y=5+0 \\ y=5 \\ \implies\text{Point (0,5)} \end{gathered}\)Similarly:
\(\begin{gathered} \text{When x=}4 \\ y=5+\sqrt[]{4} \\ y=5+2 \\ y=7 \\ \implies\text{Point (4,7)} \end{gathered}\)Similarly:
\(\begin{gathered} \text{When x=}9 \\ y=5+\sqrt[]{9} \\ y=5+3 \\ y=8 \\ \implies\text{Point (9,8)} \end{gathered}\)Next, draw a line joining the points (0,5), (4,7) and (9,8) as done below:

Using 50 random numbers given below, compute the mean and standard deviation. 0.937776 0.270012 0.243785 0.590701 0.824982 0.131805 0.879337 0.741998 0.254683 0.080259 0.419321 0.928220 0.958430 0.980182 0.263900 0.063119 0.762096 0.485612 0.662900 0.362242 0.724796 0.307736 0.305021 0.417052 0.054337 0.323357 0.069662 0.843387 0.353107 0.074262 0.735596 0.175095 0.390508 0.668932 0.029861 0.205228 0.387740 0.962169 0.646565 0.423914 0.754782 0.156719 0.773113 0.546335 0.323573 0.649740 0.214082 0.382383 0.383982 0.030539 Mean = (to 6 decimals) Standard deviation = (to 6 decimals)
Answers
The mean is 0.477514 (rounded to 6 decimal places).
The standard deviation is 0.288919 (rounded to 6 decimal places).
How to Solve the Problem?To calculate the mean and standard deviation, we will use the following formulas:
Mean = (sum of all values) / (number of values)
Standard deviation = sqrt[(sum of (value - mean)^2) / (number of values)]
Using these formulas, we can calculate the mean and standard deviation for the given set of random numbers:
Mean = (0.937776 + 0.270012 + 0.243785 + 0.590701 + 0.824982 + 0.131805 + 0.879337 + 0.741998 + 0.254683 + 0.080259 + 0.419321 + 0.928220 + 0.958430 + 0.980182 + 0.263900 + 0.063119 + 0.762096 + 0.485612 + 0.662900 + 0.362242 + 0.724796 + 0.307736 + 0.305021 + 0.417052 + 0.054337 + 0.323357 + 0.069662 + 0.843387 + 0.353107 + 0.074262 + 0.735596 + 0.175095 + 0.390508 + 0.668932 + 0.029861 + 0.205228 + 0.387740 + 0.962169 + 0.646565 + 0.423914 + 0.754782 + 0.156719 + 0.773113 + 0.546335 + 0.323573 + 0.649740 + 0.214082 + 0.382383 + 0.383982 + 0.030539) / 50 = 0.477514
Therefore, the mean is 0.477514 (rounded to 6 decimal places).
Now we will calculate the standard deviation:
Standard deviation = sqrt[((0.937776 - 0.477514)^2 + (0.270012 - 0.477514)^2 + (0.243785 - 0.477514)^2 + ... + (0.382383 - 0.477514)^2 + (0.383982 - 0.477514)^2 + (0.030539 - 0.477514)^2) / 50] = 0.288919
Therefore, the standard deviation is 0.288919 (rounded to 6 decimal places).
Learn more about mean here: https://brainly.com/question/20118982
#SPJ1
An artist wants to paint 15 pictures in three months she only starts a new picture when she is done with the previous one use repeated subtraction to show how many pictures she has to paint each month
Answers
Answer: 5
Step-by-step explanation: 15/3 is 5
Please help I need it quick!!!! Please
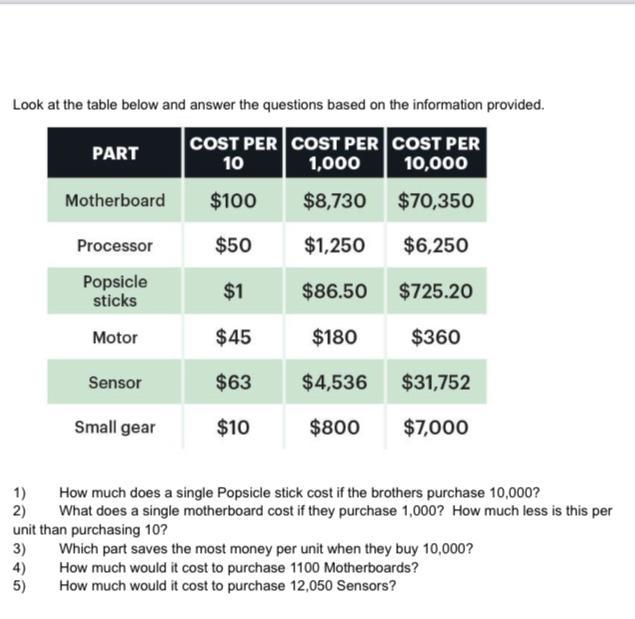
Answers
Answer:
Question 1
Cost per 10,000 Popsicle sticks = $725.20
⇒ Single Popsicle stick = 725.20 ÷ 10000 = $0.07 (nearest cent)
Question 2
Cost per 1,000 motherboards = $8,730
⇒ Cost of Single motherboard = 8730 ÷ 1000 = $8.73
Cost per 10 motherboards = $100
⇒ Cost of Single motherboard = 100 ÷ 10 = $10
Difference = 10 - 8.73 = $1.27
Question 3
Create a table with the cost per 1 unit:
\(\begin{array}{| c | c | c | c |}\cline{1-4} \sf PART & \sf COST\:PER\:1\:of\:10 & \sf COST\:PER\:1\:of\:1000 & \sf COST\:PER\:1\:of\:10000\\\cline{1-4} \sf Motherboard & \$10.00 & \$8.73 & \$7.04 \\\cline{1-4} \sf Processor & \$5.00 & \$1.25 & \$0.63 \\\cline{1-4} \sf Popsicle & \$0.10 & \$0.09 & \$0.07 \\\cline{1-4} \sf Motor & \$4.50 & \$0.18 & \$0.04 \\\cline{1-4} \sf Sensor & \$6.30 & \$4.54 & \$3.18 \\\cline{1-4} \sf Small\:gear & \$1.00 & \$0.80 & \$0.70 \\\cline{1-4} \end{array}\)
From inspection of the table, the Motor saves the most money per unit when 10,000 is bought, since the difference between the cost of 1 unit is the greatest for this part.
Question 4
Cost of 1100 motherboards
= cost of 1000 + cost of 10 x 10
= 8730 + 100 x 10
= 8730 + 1000
= $9,730
Question 5
Cost of 12050 sensors
= cost of 10000 + cost of 1000 x 2 + cost of 10 x 5
= 31752 + 4536 x 2 + 63 x 5
= 31752 + 9072 + 315
= $41,139
Sophia factored 81y^681y 6 81, y, start superscript, 6, end superscript as (9y^3)(9y^2)(9y 3 )(9y 2 )left parenthesis, 9, y, cubed, right parenthesis, left parenthesis, 9, y, squared, right parenthesis. Ahmed factored 81y^681y 6 81, y, start superscript, 6, end superscript as (3y^6)(27y)(3y 6 )(27y)left parenthesis, 3, y, start superscript, 6, end superscript, right parenthesis, left parenthesis, 27, y, right parenthesis. Which of them factored 81y^681y 6 81, y, start superscript, 6, end superscript correctly? Choose 1 answer: Choose 1 answer: (Choice A) A Only Sophia (Choice B) B Only Ahmed (Choice C) C Both Sophia and Ahmed (Choice D) D Neither Sophia nor Ahmed
Answers
Neither Sophia nor Ahmed factored 81y⁶ correctly.
What is superscript of a variable?
A superscript is a number or variable that is written in tiny script at the top right of another number or variable, according to the definition of a superscript.
Given expression is 81y⁶.
Sophia factored 81y⁶ as (9y³)(9y²).
Ahmed factored 81y⁶ as (3y⁶)(27y).
Now simplify both factors:
(9y³)(9y²)
Combine variable and numbers:
= (9×9)(y³ × y²)
= 81 (y³ × y²)
Simplify the product of the variables by formula a^m × a^n = a^(m+n):
= 81 y³⁺²
= 81y⁵
≠ 81y⁶
Now consider (3y⁶)(27y)
Combine variable and numbers:
= (3×27)(y⁶ × y)
= 81 (y⁶ × y)
Simplify the product of the variables by formula a^m × a^n = a^(m+n):
= 81y⁶⁺¹
=81y⁷
≠ 81y⁶
To learn more about factored, click on below link:
https://brainly.com/question/15652087
#SPJ1
My teacher said this is all due TODAY I need help ASAP please
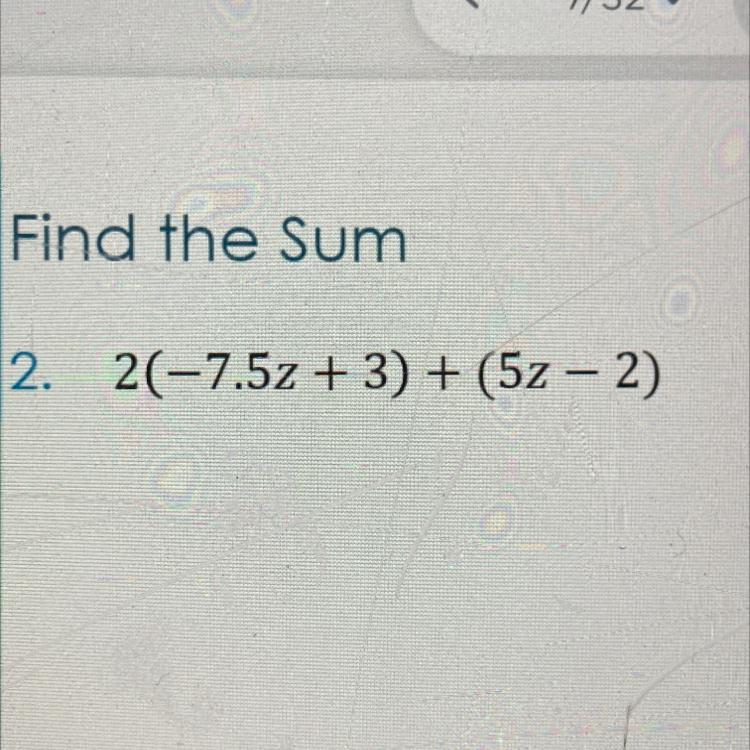
Answers
Answer:
i love you :)
Step-by-step explanation:
you just have to mutliply the first one and sum both of them
(-15z + 6) + (5z - 2)
-15z + 6 + 5z -2
= -10z + 4
о
Most TCS foods cool from O to O
Fahrenheit within two hours and O to
degrees Fahrenheit within four hours when they're stored.
This means that they are considered safe since bacterial
growth has not reached dangerous levels yet.
degrees
Submit Answer
Answers
Most TCS foods cool from 135°F to 70°F within two hours and from 70°F to 41°F within four hours when they're stored.
What temperatures should TCS foods be kept at ?TCS foods are those foods that require time and temperature control to prevent the growth of harmful bacteria and other microorganisms that can cause foodborne illness.
The general rule is that TCS foods should be cooled from 135°F to 70°F within two hours and from 70°F to 41°F within an additional four hours. This means that the total time for cooling TCS foods should not exceed six hours.
Find out more on TCS foods at https://brainly.com/question/28257373
#SPJ1
The full question is:
Fill in the blanks:
Most TCS foods cool from _________ within two hours and from _______ within four hours when they're stored. This means that they are considered safe since bacterial growth has not reached dangerous levels yet.
Martin harvested 60 kilograms of mangoes last February, twice as much in March, and 20 kilograms more in April than the combined harvest in February and March. How many kilograms of mangoes did he harvest in all? (A little side story: My sibling needs help on this and I'm not really confident in word problems. This has been my weakness since I was very young but now I can manage haha btw thanks for the help)
Answers
Answer:
Lets express this as equations to get a better idea of this situation.
let f represent February, m represent march and so on
60 mangoes in feburary
(60)2=m
m=120
120 mangoes in march
A=120+60+20
a=200
m+f+a=total amount of mangoes
60+120+200=t
380=total
Step-by-step explanation:
The total mangoes harvested by Martin is 380 kilograms.
What are word problems?A word problem in math is a math question written as one sentence or more that requires children to apply their math knowledge to a 'real-life' scenario.
Given that, Martin harvested 60 kilograms of mangoes last February, twice as much in March, and 20 kilograms more in April than the combined harvest in February and March.
We need to find the total harvested mangoes,
Let f represent February, m represent march and April be a
February = 60 mangoes
So, in March,
(60) 2 = m
m = 120
Therefore, 120 mangoes in March
A = 120+60+20
a = 200
Now, the total mangoes = 60+120+200 = 380
Hence the total mangoes harvested by Martin is 380 kilograms.
Learn more about word problems click;
https://brainly.com/question/29203255
#SPJ3
Which expression(s) will result in a quotient that is less then one? 3/4 divided by 2/3, 7/10 divided by 4/5, 7/8 divided by 1/2, 7/8 divided by 1/2, 3/4 divided by 1/3, 1/5 divided by 11/15
Answers
Given the general rule for the division of fractions:
\(\begin{gathered} \frac{a}{b}\frac{\cdot}{\cdot}\frac{c}{d}=\frac{a\cdot d}{b\cdot c} \\ b,d\ne0 \end{gathered}\)Then, in this case we have the following:
\(\begin{gathered} \frac{3}{4}\frac{\cdot}{\cdot}\frac{2}{3}=\frac{3\cdot3}{4\cdot2}=\frac{9}{8}>1 \\ \frac{7}{10}\frac{\cdot}{\cdot}\frac{4}{5}=\frac{7\cdot5}{4\cdot10}=\frac{35}{40}<1 \\ \frac{7}{8}\frac{\cdot}{\cdot}\frac{1}{2}=\frac{7\cdot2}{8\cdot1}=\frac{14}{8}>1 \\ \frac{3}{4}\frac{\cdot}{\cdot}\frac{1}{3}=\frac{3\cdot3}{4\cdot1}=\frac{9}{4}>1 \\ \frac{1}{5}\frac{\cdot}{\cdot}\frac{11}{15}=\frac{1\cdot15}{5\cdot11}=\frac{15}{55}<1 \end{gathered}\)therefore, only the second and the last options are less than 1
What is the domain of the function represented by this graph? the graph of a quadratic function y = x^2 – 4 with a minimum value at the point (0,-4) A. -2 ≤ x ≤ 2 B. x ≥ 4 C. x ≤ 0 D. all real numbers Reset
Answers
Domain of the function represented by the graph of a quadratic function y = \(x^2\) – 4 with a minimum value at the point (0,-4) is all real numbers.
The correct answer is option D.
To determine the domain of the quadratic function y = \(x^2\) - 4, we need to consider the x-values for which the function is defined. Since a quadratic function is defined for all real numbers, the domain of this function is "all real numbers."
Let's analyze the given function and its graph to understand why the domain is "all real numbers."
The function y = \(x^2\) - 4 represents a parabola that opens upward, which means it extends infinitely in both positive and negative x-directions. The vertex of the parabola is at the point (0, -4), indicating that the minimum value of the function occurs at x = 0.
Since there are no restrictions or limitations on the x-values for which the function is defined, the domain is unrestricted and encompasses all real numbers. In other words, the function can be evaluated and calculated for any real value of x, whether it is a negative number, zero, or a positive number.
For more such information on: quadratic function
https://brainly.com/question/29293854
#SPJ8
The Venn diagram below shows information about the number of items in sets T and V.
An item is chosen at random.
Given that P(TIV) = j

Answers
The value of x from the venn diagram if P(T | V) = 1/5 is 16
How to determine the value of x
From the question, we have the following parameters that can be used in our computation:
The venn diagram
From the venn diagram, we have the following probability values
P(T | V) = (x - 4)/(3x + x - 4)
Evaluate the like terms
So, we have
P(T | V) = (x - 4)/(4x - 4)
From the question, we have
P(T | V) = 1/5
This means that
(x - 4)/(4x - 4) = 1/5
When evaluated, we have
x = 16
Hence, the value of x is 16
Read more about probability at
https://brainly.com/question/31649379
#SPJ1
PRE CALC HELP NEEDED

Answers
Answer:
\(\dfrac{5e^2}{2}\)
Step-by-step explanation:
Differentiation is an algebraic process that finds the slope of a curve. At a point, the slope of a curve is the same as the slope of the tangent line to the curve at that point. Therefore, to find the slope of the line tangent to the given function, differentiate the given function.
Given function:
\(y=x^2\ln(2x)\)
Differentiate the given function using the product rule.
\(\boxed{\begin{minipage}{5.5 cm}\underline{Product Rule for Differentiation}\\\\If $y=uv$ then:\\\\$\dfrac{\text{d}y}{\text{d}x}=u\dfrac{\text{d}v}{\text{d}x}+v\dfrac{\text{d}u}{\text{d}x}$\\\end{minipage}}\)
\(\textsf{Let\;$u=x^2}\)\(\textsf{Let\;$u=x^2$}\implies \dfrac{\text{d}u}{\text{d}x}=2x\)
\(\textsf{Let\;$v=\ln(2x)$}\implies \dfrac{\text{d}v}{\text{d}x}=\dfrac{2}{2x}=\dfrac{1}{x}\)
Input the values into the product rule to differentiate the function:
\(\begin{aligned}\dfrac{\text{d}y}{\text{d}x}&=u\dfrac{\text{d}v}{\text{d}x}+v\dfrac{\text{d}u}{\text{d}x}\\\\&=x^2 \cdot \dfrac{1}{x}+\ln(2x) \cdot 2x\\\\&=x+2x\ln(2x)\end{aligned}\)
To find the slope of the tangent line at x = e²/2, substitute x = e²/2 into the differentiated function:
\(\begin{aligned}x=\dfrac{e^2}{2}\implies \dfrac{\text{d}y}{\text{d}x}&=\dfrac{e^2}{2}+2\left(\dfrac{e^2}{2}\right)\ln\left(2 \cdot \dfrac{e^2}{2}\right)\\\\&=\dfrac{e^2}{2}+e^2\ln\left(e^2\right)\\\\&=\dfrac{e^2}{2}+2e^2\\\\&=\dfrac{5e^2}{2}\end{aligned}\)
Therefore, the slope of the line tangent to the graph of y = x²ln(2x) at the point where x = e²/2 is:
\(\boxed{\dfrac{5e^2}{2}}\)
Standard form of y=7x+10
Answers
Answer: 7x-y=10
Step-by-step explanation:
Craig’s Computer Supply Shop sells color ink printer cartridges for $24.99 and black ink printer cartridges for $14.99. Last week the store sold a total of 27 ink cartridges. If the sales income for these items was $514.73, not including tax, which of these conclusions is reasonable?
A.) There were more black ink cartridges than color ink cartridges sold last week.
B.) There were more color ink cartridges than black ink cartridges sold last week
C.) The total sales income, not including tax, for color ink cartridges was $399.84
D.) The total sales income, not including tax, for black ink cartridges was $164.89
Answers
There were more color ink cartridges than black ink cartridges sold last week. Therefore, option B is the correct conclusion.
What is system of equation?A system of equations, sometimes referred to as an equation system or a set of simultaneous equations, is a finite set of equations for which we searched for common solutions. Variables are related to one another specifically in each equation in a system of equations. To discover a set of variable values that satisfy each equation, the equations can be solved simultaneously.
In everyday situations where the unknown values can be represented as variables, a system of linear equations is used to model the problem. Many techniques, including substitution, elimination, graphing, etc., are used to solve systems of equations.
Let us suppose the number of color ink cartridges sold = x.
The number of color ink cartridges sold = y.
Thus,
x + y = 27
24.99x + 14.99y = 514.73
Multiplying the first equation by 24.99 and subtracting it from the second equation multiplied by 100, we get:
1499y = 1813
y ≈ 1.21
Substituting y back into the first equation, we get:
x ≈ 25.79
Hence, there were more color ink cartridges than black ink cartridges sold last week. Therefore, option B is the correct conclusion.
Learn more about system of equation here:
https://brainly.com/question/24065247
#SPJ1
NO LINKS!!!! URGENT HELP PLEASE!!!
Please help me with these problems


Answers
Answer:
\(\sf g(x) = f(x\; \boxed{+ 3}\;) \;\boxed{- 6}\)
Step-by-step explanation:
A translation is a transformation that moves every point of a figure the same distance and in the same direction. This means that the size, shape, and orientation of the figure are preserved, but its position is changed.
From inspection of the given diagram, we can see that the size, shape and orientation of the graph of function g is the same as that of the graph of function f, but its position has changed. Therefore, the transformation is a translation.
We can use the vertex of both graphs to determine the translation.
The vertex of function f is the origin (0, 0).The vertex of function g is (-3, -6).Therefore, the graph of function f has been moved 3 units left and 6 units down to create the graph of function g.
When we move "a" units left, we add the value of "a" to the x-value of the function.
When we move "a" units down, we subtract the value of "a" from the function.
Therefore:
\(\sf g(x) = f(x\; \boxed{+ 3}\;) \;\boxed{- 6}\)
I really need some heeeeeeeeeeeeeeeeeeeeeeelp 50 points
based on the smallest dragonboy

Answers
are we suppose to make a story or something
Answer:
This question makes 0 sense! how do i even answer?
