Suppose that a category of world class runners are known to run a marathon (26 miles) in an average of 146 minutes with a standard deviation of 11 minutes. Consider 49 of the races. Let x = the average of the 49 races. Part (a) two decimal places.) Give the distribution of X. (Round your standard deviation to two decimal places)Part (b) Find the probability that the average of the sample will be between 144 and 149 minutes in these 49 marathons. (Round your answer to four decimal places.) Part (c) Find the 80th percentile for the average of these 49 marathons. (Round your answer to two decimal places.) __ min Part (d) Find the median of the average running times ___ min
Answers
(a)The distribution of X (the average of the 49 races) follows a normal distribution with mean 146 minutes and standard deviation 11 minutes. (b)The probability of the average of the sample being between 144 and 149 minutes is 0.5854.(c)The 80th percentile for the average of these 49 marathons is 157.2 minutes.(d) The median of the average running times is 146 minutes.
Part(a) The distribution of X (the average of the 49 races) follows a normal distribution with mean 146 minutes and standard deviation 11 minutes. Part (b) The probability that the average of the sample will be between 144 and 149 minutes in these 49 marathons can be calculated using the z-score formula: z = (x - mean)/standard deviation
For x = 144, z = (144 - 146)/11 = -0.18
For x = 149, z = (149 - 146)/11 = 0.27,using the z-score table, the probability of the average of the sample being between 144 and 149 minutes is 0.5854 (0.4026 + 0.1828).
Part (c) The 80th percentile for the average of these 49 marathons can be calculated using the z-score formula: z = (x - mean)/standard deviation, For the 80th percentile, z = 0.84 (from z-score table). Therefore, x = 146 + (0.84 * 11) = 157.2 minutes. Part (d) The median of the average running times is 146 minutes. The median is the midpoint of the data which means half of the data is above the median and half of the data is below the median. Therefore, the median of the average running times is equal to the mean.
Read more about statistics at
https://brainly.com/question/30655485
#SPJ11
Related Questions
Question 5 About 9% of the population has a particular genetic mutation. 500 people are randomly selected. Find the standard deviation for the number of people with the genetic mutation in such groups of 500. Round your answer to three decimal places
Answers
Therefore, the standard deviation for the number of people with the genetic mutation in groups of 500 is approximately 6.726.
To find the standard deviation for the number of people with the genetic mutation in groups of 500, we can use the binomial distribution formula.
Given:
Probability of having the genetic mutation (p) = 0.09
Sample size (n) = 500
The standard deviation (σ) of a binomial distribution is calculated using the formula:
σ = √(n * p * (1 - p))
Substituting the given values:
σ = √(500 * 0.09 * (1 - 0.09))
Calculating the standard deviation:
σ ≈ 6.726 (rounded to three decimal places)
To know more about standard deviation,
https://brainly.com/question/12991013
#SPJ11
What is the maximum of thisgraph over the interval [-4, 4]?
Answers
The maximum of a graph is found on the y axis. Considering the given interval, the point on the y axis is 4. Thus, the maximum of the graph over the interval is 4.
i need help on this i would appreciate you soo much!!

Answers
Answer:
2(-3x+2)^2 -1
Step-by-step explanation:
so first you would find that f(g(x)) = f(-3x+2)
next plug in
f(-3x+2) = 2x^2-1
to every x
f(-3x+2) = 2(-3x+2)^2-1
Tammy has a rectangular poster. The poster is 1.2 meters long and 0.9 meters wide. What is the area of the poster in square centimeters? Do not round your answer. Be sure to include the correct unit in your answer.
Answers
Answer:
HOI
Step-by-step explanation:
I don’t know this question
Help me

Answers
Answer: Probably negative 69
1) the lowest point of the cable is at 27 meters above the deck
2) the span of the bridge is 1 meters long
3) the lowest point of the cable is at 1 meters above the deck
4) the span of the bridge is 27 meters long
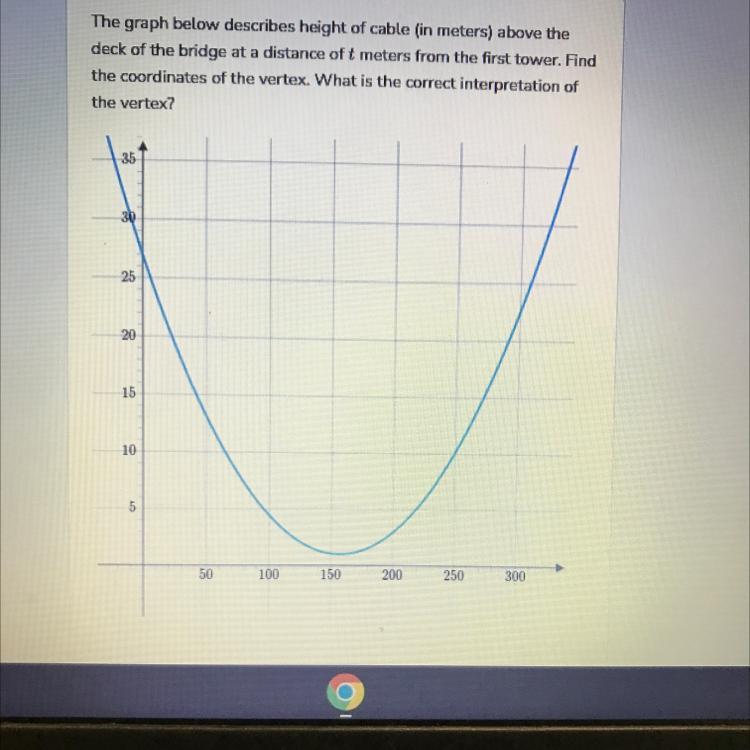
Answers
The coordinates of the vertex are (0, 27).
Describe Parabola?A parabola is a symmetrical, U-shaped curve that can be formed by intersecting a cone with a plane that is parallel to one of its sides. In mathematics, a parabola is a type of quadratic function that can be written in the standard form y = ax² + bx + c, where x and y are variables, a is the coefficient of the x² term, b is the coefficient of the x term, and c is the constant term. The coefficient a determines the shape of the parabola: if a is positive, the parabola opens upwards and if a is negative, the parabola opens downwards.
To find the vertex of the parabola, we need to use the formula:
x = -b / 2a
where a and b are the coefficients of the quadratic equation in standard form (ax² + bx + c), which describes the parabola.
In this case, the equation of the parabola can be written as:
h = -0.045t² + 27
where h is the height of the cable (in meters) above the deck of the bridge, and t is the distance (in meters) from the first tower.
By comparing this equation with the standard form, we can see that a = -0.045 and b = 0. To find the vertex, we can substitute these values into the formula:
x = -b / 2a = 0 / (-2 * 0.045) = 0
So the x-coordinate of the vertex is 0. To find the y-coordinate, we can substitute this value back into the equation:
h = -0.045(0)² + 27 = 27
So the coordinates of the vertex are (0, 27).
The correct interpretation of the vertex is that it represents the highest point on the parabola, which in this case is the highest point of the cable above the deck of the bridge. The vertex is also the axis of symmetry of the parabola, which means that the distance from the first tower to the vertex is the same as the distance from the vertex to the second tower.
To know more about equation visit:
https://brainly.com/question/27886219
#SPJ1
PLEASE HELP which equation in the word bank can solve for x ?


Answers
Answer:
x + 10 = 24
Step-by-step explanation:
In the figure attached,
There are two external points A and B.
Fro point A two tangents AD and AE have been drawn and From point B tangents BE and BC have been drawn.
Since AD = 10 units,
Therefore, AE = 10 units
(Since tangents drawn from a point to a circle are same in measure, therefore, AD = AE)
Therefore,
BE = AB - AE
Since BE = BC
So BC = AB - AE
x = 24 - 10
x + 10 = 24
Therefore, (x + 10) = 24 will be the equation to be used to solve for x.

determine which point from the specified set satisfies the system of equations. y=3x−3 and y=−x 2
Answers
There are two points that satisfy the system of equations:
(0.79, 0.37)
(-3.79, -12.37)
The system of equations is:
y = 3x - 3
y = -x^2
To determine which point from a specified set satisfies the system of equations, we need to find the values of x and y that satisfy both equations simultaneously.
Substituting y = 3x - 3 into the second equation, we get:
3x - 3 = -x^2
Rearranging this equation, we get:
x^2 + 3x - 3 = 0
Using the quadratic formula, we can solve for x:
x = (-3 ± sqrt(3^2 - 41(-3))) / (2*1) = (-3 ± sqrt(21)) / 2
Therefore, there are two possible values of x that satisfy the system of equations:
x = (-3 + sqrt(21)) / 2 ≈ 0.79
x = (-3 - sqrt(21)) / 2 ≈ -3.79
To find the corresponding values of y, we can substitute these values of x into either equation. For example, if we use y = 3x - 3, we get:
y ≈ 0.37 (when x ≈ 0.79)
y ≈ -12.37 (when x ≈ -3.79)
Therefore, there are two points that satisfy the system of equations:
(0.79, 0.37)
(-3.79, -12.37)
To know more about Equations :
https://brainly.com/question/13865224
#SPJ11
In the Japanese game show Sushi Roulette, the contestant spins a large wheel that’s divided into 12 equal sections. Nine of the sections have a sushi roll, and three have a “wasabi bomb.” When the wheel stops, the contestant must eat whatever food is on that section. To win the game, the contestant must eat one wasabi bomb. Find the probability that it takes 3 or more spins for the contestant to get a wasabi bomb. Show your method clearly.
Answers
Answer:
P = 0.545
Step-by-step explanation:
Here we can find the probability Q, in which you need one or two spins to win the game, and then:
P = 1 - Q
Will be the probability that it takes 3 or more spins to win.
Case where you need only one spin:
There are 3 out of 12 possible outcomes, then the probability of winning with only one spin is:
p = 3/12.
Case where you need two spins to win:
Here we should get a normal sushi roll in the first spin and a wasabi bomb in the second.
The probability of getting a sushi roll in the first spin is equal to the quotient between the number of sushi rolls (9) and the total number of possible outcomes (12), then:
p1 = 9/12
For the second spin we need to get a wasabi bomb, assuming that the susi roll is not replaced (so now there are 8 sections with sushi rolls and 3 with wasabi bombs, if you get the empty section you roll again or something like that)
Now the probability of getting a wasabi bomb is equal to the quotient between the number of wasabi bombs remaining (3) and the total number of outcomes remaining (11), this is:
p2 = 3/11
The joint probability is the product of the two individual probabilities:
p = p1*p2 = (9/12)*(3/11)
Now, the total probability of winning with one or two spins is equal to the sum of the probabilities for each case, then:
Q = (9/12)*(3/11) + 3/12 = 0.455
Then the probability of needing 3 or more spins to win is:
P = 1 - Q = 1 - 0.455 = 0.545
The probability that it takes 3 or more spins for the contestant to get a wasabi bomb is 0.545 and this can be determined by using the given data.
Given :
In the Japanese game show Sushi Roulette, the contestant spins a large wheel that’s divided into 12 equal sections. Nine of the sections have a sushi roll, and three have a wasabi bomb.When the wheel stops, the contestant must eat whatever food is on that section. To win the game, the contestant must eat one wasabi bomb.The probability to win the game in the first spin is:
\(\rm P_1=\dfrac{3}{12}=\dfrac{1}{4}\)
The probability to win the game in the second spin is:
\(\rm P_2 = \dfrac{9}{12}\times \dfrac{3}{11}\)
\(\rm P_2=\dfrac{9}{44}\)
The probability to win in 1 or 2 spins is given by:
\(\rm Q = P_1+P_2=\dfrac{9}{44}+\dfrac{1}{4}\)
Q = 0.455
So, the probability that it takes 3 or more spins for the contestant to get a wasabi bomb is:
P = 1 - Q
P = 1 - 0.455
P = 0.545
For more information, refer to the link given below:
https://brainly.com/question/795909
a. What is the nth fraction in the following sequence? 2
1
, 4
1
, 8
1
, 16
1
, 32
1
,… b. What is the sum of the first n of those fractions? To what number is the sum getting closer and closer? Two forces, A=80 N and B=44 N, act in opposite directions on a box, as shown in the diagram. What is the mass of the box (in kg ) if its acceleration is 4 m/s 2
?
Answers
A)an = 2*2^(n-1)`. B) `The sum of the first n fractions is `2*(2^n - 1)`.
a. The sequence is a geometric sequence with the first term `a1 = 2` and common ratio `r = 2`.Therefore, the nth term `an` is given by:`an = a1*r^(n-1)`
Substituting `a1 = 2` and `r = 2`, we have:`an = 2*2^(n-1)`
b. To find the sum of the first n terms, we use the formula for the sum of a geometric series:`S_n = a1*(1 - r^n)/(1 - r)
`Substituting `a1 = 2` and `r = 2`, we have:`S_n = 2*(1 - 2^n)/(1 - 2)
`Simplifying:`S_n = 2*(2^n - 1)
`The sum of the first n fractions is `2*(2^n - 1)`.As `n` gets larger and larger, the sum approaches `infinity`.
Thus, the sum is getting closer and closer to infinity.
Know more about sequence here,
https://brainly.com/question/30262438
#SPJ11
A student used a 30% coupon to buy a pair of jeans. There was no tax. The student paid $67.34. What was the original price of the jacket?
Answers
Answer:
$80 is the 100% original price
The sale price is $56 with 30% off and $24 in savings.
Step-by-step explanation:
We can write a proportion. We know that $24 is a 30% off discount of an unknown original price. Let's call it x. We write equal ratios of comparing percent and comparing the 24 to the original price. We then set them equal.
We then cross multiply across the equal sign from numerator to the opposite numerator.
30(x)=24(100)
30x=2400
We divide to find x.
x=80.
Since we saved $24 as a discount, the sale price would be 80-24=56.
The number of messages that arrive at a Web site is a Poisson distributed random variable with a mean of 5 messages per hour. Round your answers to four decimal places.(a) What is the probability that 5 messages are received in 1 hour?(b) What is the probability that 10 messages are received in 1.5 hours?(c) What is the probability that less than 2 messages are received in 1/2 hour?
Answers
The probability that 5 messages are received in 1 hour is is 0.1755 ,the probability that 10 messages are received in 1.5 hours is 0.0858 and the probability that less than 2 messages are received in 1/2 hour is 0.2873
Let X shows the number of messages received per hour. The pdf of X is
\(P(X=x)=\) \(\frac{e^{-5}\cdot 5^{x}}{x!},x=0,1,2,3,....\)
Therefore, the probability that 5 messages are received in a single hour is
\(P(X=5)=\frac{e^{-5}\cdot 5^{5}}{5!}=0.1755\)
(b) Number of message received in 1 hour is 5 so number of message received in 1.5 hour is 7.5. So the probability that 10 messages are received in 1.5 hours is
\(P(X=10)=\frac{e^{-7.5}\cdot 7.5^{10}}{10!}=0.0858\)
(c) Number of message received in 1 hour is 5 so number of message received in 1/2 hour is 2.5. So the probability that less than 2 messages are received in 1/2 hour is
\(P(X < 2)=\frac{e^{-2.5}\cdot 2.5^{0}}{0!}+\frac{e^{-2.5}\cdot 2.5^{1}}{1!}=0.2873\)
Learn more about probability
brainly.com/question/30034780
#SPJ4
70% of the shoes in the UK are made abroad. if you survey 120 people about the shoes they are wearing, how many do we expect to have UK-made shoes?
Answers
Answer:
84
Step-by-step explanation:
70% of 120= 84
rite the composite function in the form f(g(x)). [identify the inner function u = g(x) and the outer function y = f(u).] y = 3 1 4x (g(x), f(u)) =
Answers
The composite function in the form f(g(x)) is f(g(x)) = 3(1 + 4x), with the inner function g(x) = 1 + 4x and the outer function f(u) = 3u.
Given the function y = 3(1 + 4x), we need to write it in the form f(g(x)) by identifying the inner function g(x) and the outer function f(u).
First, let's identify g(x), which is the inner function. In this case, g(x) = 1 + 4x.
Next, let's identify the outer function f(u). Since y = 3(1 + 4x), we can rewrite this expression as y = 3u, where u = 1 + 4x. So, f(u) = 3u.
Now, we can write the composite function in the form f(g(x)): f(g(x)) = f(1 + 4x) = 3(1 + 4x).
So, the composite function in the form f(g(x)) is f(g(x)) = 3(1 + 4x), with the inner function g(x) = 1 + 4x and the outer function f(u) = 3u.
To learn more about composite function here:
brainly.com/question/5614233#
#SPJ11
The lengths of two sides of a triangle are 4 cm and 13 cm. Identify the range of possible lengths for the third side.
Answers
Answer:
9cm<x<17cm
Step-by-step explanation:
your welcome
The range of the possible lengths for the third side is 9 cm < x < 17 cm.
What is Triangle?A triangle is a geometrical shape which has three vertices, three edges and three angles. In other words, in Euclidean geometry, a triangle is defined as a two dimensional shape which is three non-collinear points lying on a unique plane.
The sum of the interior angles of a triangle is 180 degrees.
Here we have lengths of two sides of a triangle which are 4 cm and 13 cm.
If the length of two sides of a triangle are given, then the length of third side will lie in the range between the difference of the other two sides and the sum of the other two sides.
Let x represents the third side of the triangle.
So, here the third side lies between 13 cm - 4 cm and 13 cm + 4 cm.
13 - 4 < x < 13 + 4
9 < x < 17
Hence the range of possible lengths for the third side of the triangle is in between 9 cm < x < 17 cm.
To learn more about Triangles, click:
https://brainly.com/question/2773823
#SPJ2
hey! please help on this question i'll give brainliest <333 .

Answers
Answer:
C, the third choice
Step-by-step explanation:

Please help! This is past due and i need it in in like 30 minutes. Ill be posting more questions soon so stay here.


Answers
Answer:
384 square inches
Step-by-step explanation:
The side is 10×5=50
There are 4 sides of equal surface area so we are at 200
The floor is 8×10=80 so we are at 280
The front is 8×5=40 and the back is the same so add another 40 so we are at 360
Add the little triangles which are 4×3=12 and you add the back as well so we get 384 square inches
Find the area & perimeter of each triangle
‼️ASAP!!! BRAINLIEST!!‼️
PLS HELP + EXPLAIN!!! Thx!
(NO LINKS PLEASE)

Answers
Answer:
I think it is the first one because it shows 18 but it says the nearest tenth so it will become 20
A 40 gram sample of a substance that’s used for drug research has a k-value of 0.1472.
Find the substance’s half-life, in days. Round your answer to the nearest tenth.
Answers
A 40 gram sample of a substance that’s used for drug research has a k-value of 0.1472. The substance's half-life, in days, is approximately 4.7 days.
The half-life of a substance is the time it takes for half of the substance to decay or undergo a transformation. The half-life can be determined using the formula:
t = (0.693 / k)
where t is the half-life and k is the decay constant.
In this case, we are given that the sample has a k-value of 0.1472. We can use this value to calculate the half-life.
t = (0.693 / 0.1472) ≈ 4.7 days
Therefore, the substance's half-life, rounded to the nearest tenth, is approximately 4.7 days.
For more such questions on k-value, click on:
https://brainly.com/question/1978047
#SPJ8
if a is an n × n matrix such that a = p dp −1 with d diagonal and p invertible, then the columns of p must be eigenvectors of a.T/F
Answers
False. The columns of matrix P are not necessarily eigenvectors of matrix A. While the diagonal matrix D contains the eigenvalues of A, the eigenvectors are not explicitly determined by the columns of P.
False. The columns of matrix P are not guaranteed to be eigenvectors of the transpose of matrix A (A.T).
In the given equation, \(a = PDP^(-1),\)
where D is a diagonal matrix and P is an invertible matrix.
The diagonal elements of D represent the eigenvalues of matrix A, while the columns of P correspond to the eigenvectors of A.
When considering the transpose of matrix A (A.T), we have \((A.T) = (PDP^(-1)).T = (P^{(-1)})^T D^T P^T.\)
Taking the transpose of a product involves reversing the order of the matrices and transposing each matrix individually.
Therefore, we have \((A.T) = P^T D^T (P^{(-1)})^T.\)
Since P is an invertible matrix, its transpose \(P^T\) is also invertible. Similarly, the transpose of the inverse of \(P, (P^{(-1)} )^T,\) is also invertible.
However, the key point is that the diagonal matrix\(D^T\) is not guaranteed to have the same eigenvalues as matrix A.
The eigenvalues of A are present in D, but they may not remain on the main diagonal after transposing.
Thus, the columns of matrix P, which correspond to the eigenvectors of A, may not necessarily be the eigenvectors of A.T.
In conclusion, the statement is false.
The columns of matrix P do not have to be eigenvectors of the transpose of matrix A (A.T).
For similar question on matrix.
https://brainly.com/question/30292829
#SPJ11
a recent study of cardiovascular risk factors reported that 30% of adults met criteria for hypertension. if 15 adults are assessed, what is the probability that a. exactly 5 meet the criteria for hypertension? b. none meet the criteria for hypertension c. how many would you expect to meet the criteria for hypertension?
Answers
On solving the provided question, we got to know that - 40/155 adults will not have hypertension (70%),
How is probability calculated?The probability is calculated by dividing the total number of outcomes by the total number of possible ways an event may occur. Probability and odds are two different ideas. The chances are calculated by dividing the likelihood that a certain event will occur by the likelihood that it won't.
What is probability?Probabilities are mathematical explanations of the chance that an event will happen or that a proposition is true. The probability of an occurrence is a number between 0 and 1, where 0 often indicates impossibility and 1 normally indicates certainty.
To know more about probability visit:
https://brainly.com/question/15124899
#SPJ4
I will give BRAINLIEST to the correct answer
Find the measure of

Answers
Answer: SOLN,
let,<FHC be x
<GHC+<FHC( sum of angle of triangle=180 degree
x+6m+55+8m+55=180
x+ 14m+110=180
x+14m=180-110
x+14m=70
x=70 divied by 14m
x=5m
therefore,the value of <FHC is 5m.
b
Determine if the following statement is true or false: Children are typically
introduced to video games between the ages of six and eight. Explain your answer
using data from the graph. (2 points)

Answers
Answer:
The following statement, “Children are typically introduced to video games between the ages of six to eight” is a true statement. The graph shows that a very small percentage of children from birth to five years old play video games, but suddenly, once they have turned 6, there is practically a 60% increase in how many kids are playing video games one hour a week. It is from the age 6 that the kids start off and are introduced to the video games, as more and more kids end up playing as well as the grow older.
Step-by-step explanation:
change wording
We can easily conclude from the column chart that children at the age group of 6-8 are introduced to video games typically.
What is column chart?
''A column chart is a data visualization where each category is represented by a rectangle, with the height of the rectangle being proportional to the values being plotted. Column charts are also known as vertical bar charts.''
From the column chart, it is clear that children of age groups of 0-2 and 3-5 are using almost minimum amount of video games. The percentage is near about (0 - 5%).
After that, the children of the age group of 6-8 are using video games for a much longer period as compared to the previous two groups. The percentage is 60%.
After that, the next children of the age group of 9-11 are using video games for a much slightly more as compared to the previous group. The percentage is around 65%
The children of the age group of 12-14 are using video games for a slightly longer period as compared to the previous group. The percentage is about 75%.
The children of the age group of 15-17 are using video games for a maximum period in this graph. The percentage is 80%.
We can easily conclude from the column chart that children at the age group of 6-8 are introduced to video games typically. Because, before that age there were not much playing of video games as per the given column chart .
Learn more about column chart here: https://brainly.com/question/26501836
#SPJ2
How many different batting orders can be formed for a 9-member baseball team?
Hint: Assume all team members are in the batting order
Answers
Answer:
362,880 different
Step-by-step explanation:
Use the permutation 9*8*7*6*5*4*3*2*1. Since there are 9 possible players for the first position, 8 for the 2nd (1 is taken off), 7 for the 3rd, etc. So you would multiply these numbers together. So there are 362,880 different possible batting orders.
A rectangular closet has an area of 36 square feet and a perimeter of 24 feet. What are the dimensions of the closet?
Answers
The dimension of the rectangular closet are as follows:
width = 6 ftlength = 6 ftHow to find the dimension of a rectangular closet?A rectangular closet has an area of 36 square feet and a perimeter of 24 feet. The dimension of the closet is as follows:
perimeter of the rectangular closet = 2(l + w)
where
l = lengthw = width24 = 2(l + w)
l + w = 12
l = 12 - w
Area of the rectangular closet = lw
where
l = lengthw = widthTherefore,
36 = lw
Using substitution,
36 = (12 - w)w
36 = 12w - w²
w² - 12w + 36 = 0
w² - 6w - 6w + 36 = 0
w(w - 6) - 6(w - 6) = 0
(w - 6)(w - 6) = 0
Therefore,
w = 6
l = 36 / 6
l = 6
Hence,
length = 6ft
width = 6 ft
learn more on rectangle here: https://brainly.com/question/26493750
#SPJ1
Please help!! How do I Plot the point (1.5, -3.5) on the coordinate plane.

Answers
Answer:
Step-by-step explanation: since the 1.5 is suppose to be on the x axis, you plot the point between 1 and 2. Ten you go down to the y axis since it is negative and plot it between -2 and -3.
click the file below to see the answer:

Which of the following statements is not true about a rational function of the form f(x) where g and h are polynomial functions? O A. The graph of a rational function will never intersect a vertical asymptoto. OB. A rational function may have many vertical asymptotes. Ос. If the degree of gism and the degree of his n such that , then will have a horizontal asymptote with equation where is the leading coefficient of a and bm is the leading coefficient of h. D. A rational function mav have many horizontal asymptotes.
Answers
The statement that is not true about a rational function of the form f(x) where g and h are polynomial functions is D. A rational function may have many horizontal asymptotes.
A rational function is defined as the ratio of two polynomial functions, where g and h are polynomials and h is not the zero polynomial. The graph of a rational function can have vertical asymptotes, which occur when the denominator of the function is equal to zero. However, a rational function can intersect a vertical asymptote if the numerator is also equal to zero at that point.
Regarding vertical asymptotes, statement A is true. The graph of a rational function will never intersect a vertical asymptote, as long as the function is defined at that point.
Statement B is also true. A rational function may have multiple vertical asymptotes if the denominator has multiple factors that result in the function being undefined at different points.
Statement C is also true. If the degrees of g and h are m and n, respectively, and m is less than or equal to n, then the rational function will have a horizontal asymptote with an equation of y = (a/b).
However, statement D is not true. A rational function can have at most one horizontal asymptote, and this occurs when the degree of g is equal to the degree of h. The equation of the horizontal asymptote is y = (a/b), where a is the leading coefficient of g and b is the leading coefficient of h.
Learn more about denominator here: https://brainly.com/question/15007690
#SPJ11
Consider the following set of numbers:
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
What is the probability of drawing an odd number or a
multiple of 3?

Answers
Answer:
Probability of drawing an odd number.
Number of odd numbers = 5
Number of numbers in the set = 10
So it's a 5 in 10 chance or 1 in 2 chance.
Probability of drawing a multiple of 3.
Multiples of 3 in the set = 3, 6 and 9 = 3 multiples of 3
Number of numbers in the set = 10
So it's a 3 in 10 chance
Let Fi F(z) = 2 ² + ²/2 - ²2-1 (a) Find M=max ₁21=1 / F(Z) | Fizi=1 (b) = 2€ B₂ (0) such that | F(2₂) 1=M? Is there any contradiction with the maximum modulus principle?
Answers
The problem involves finding the maximum value of the function F(z) = 2z² + z/(2 - z²) - z² - 1 for |z| = 1 and determining if there exists a point z₀ in the disk B₂(0) such that |F(z₀)| = M. We will explore whether this contradicts the maximum modulus principle.
To find the maximum value of F(z) on the circle |z| = 1, we need to evaluate the function F(z) along the curve parameterized by z = e^(iθ), where θ ranges from 0 to 2π. By substituting z = e^(iθ) into F(z), we obtain a function in terms of θ. Taking the absolute value of this function yields |F(z)|.
To find the maximum value of |F(z)| on the unit circle, we can evaluate |F(z)| at different points along the circle and determine the maximum. Let M be the maximum value of |F(z)| obtained in this manner.
Next, we consider the disk B₂(0) and seek a point z₀ in the disk such that |F(z₀)| = M. If such a point exists, it would imply that |F(z)| takes its maximum value on the boundary of the disk, violating the maximum modulus principle. However, it is unclear from the given information whether such a point exists.
In summary, we determine the maximum value M of |F(z)| on the unit circle |z| = 1. We then consider the disk B₂(0) to check if there exists a point z₀ in the disk such that |F(z₀)| = M. This analysis will help us ascertain if there is any contradiction with the maximum modulus principle, which states that a holomorphic function cannot attain its maximum on the interior of its domain.
Learn more about modulus here:
https://brainly.com/question/32070235
#SPJ11
Quadratic Equation Applications
The High School theatre seats 1,200 people. The next school play is approaching and the drama teacher is trying to decide how much he should charge for each ticket to the play. He normally charges $5.00 a ticket but is thinking of raising the price for the next play as the plays have been sold out in the past. He estimates that for every $0.50 raise in ticket prices he will sell 100 fewer tickets. What ticket price will maximize profits?
Let x = Number of $0.50 increases to the ticket price
Step #1) Write an expression that represents the price of each ticket depending on the price increase
Step #2) Write an expression that represents the number of tickets sold
Step #3) The money they earn is the product of the number of tickets sold and the price per ticket. Write an equation representing this amount using the equations above.
Please show your work/explain the steps taken!
Answers
The number of $0.50 increases to maximize the profit is X = 1.
First of all, we need to write the linear function which represents the price of the ticket for each increase of $0.50:
P - Price of each ticket.
x - number of increases.
We know that the current price is $5.00, so:
\(P(x) = 0.5x + 5.00\)
After that, let's build a linear function which shows the number of tickets sold for each price increase:
T - number of tickets.
x - number of increases.
\(T(x) = -100x + 1200\)
With all this done, we can finally build the quadratic function which represents the money earned:
M - money earned
\(M = Tickets Sold \times TicketPrice\\\\M = T(x) \times P(x)\\\\M = (0.5x + 5) \times (-100x + 1200)\\\\M = -50x^{2} + 600x -500x + 6000\\\\M(x) = -50x^{2} + 100x + 6000\\\\\)
Now, to finish, we only have to calculate the value of X(number of increases) which can give us the maximum value of this function:
the X coordinate for the maximum value of a quadratic is expressed by:
\(Xmax = \frac{-b}{2a} \\\\\)
In our equation, b = 100 and a = - 50 :
\(Xmax = \frac{-(100)}{2(-50)} \\\\Xmax = \frac{-100}{-100} \\\\Xmax = 1\)
Thus, the number of increases which maximizes the profit is 1.
Learn more about linear and quadratic functions in: brainly.com/question/4119784