The population of Australia was 14.692 million in 1980 and 17.065 million in 1990. Estimate the population of Australia in 2000.
Answers
The population of Australia in 2000 is estimated to be 19.438 million.
What is an equation?An equation is a mathematical statement that is made up of two expressions connected by an equal sign.
We have,
The population in 1980 = 14.692 million
The population in 1990 = 17.065 million
The change in the population from 1980 to 1990:
= 17.065 - 14.692
= 2.373
This means in 10 years there is an increase of 2.373 million.
The population estimated in 2000:
= 17.065 + 2.373
= 19.438 million
Thus,
The population of Australia in 2000 is estimated to be 19.438 million.
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ1
Related Questions
the number of hours worked per year per person in a state is normally distributed with a standard deviation of 39. a sample of 15 people is selected at random, and the number of hours worked per year per person is given below. calculate the 98% confidence interval for the mean hours worked per year in this state. round your answers to the nearest integer and use ascending order. time 2051 2061 2162 2167 2169 2171 2180 2183 2186 2195 2196 2198 2205 2210 2211 provide your answer below:
Answers
Using a t-distribution with 14 degrees of freedom (n-1) and a 98% confidence level (α = 0.02/2 = 0.01 for each tail), we have:
sample mean (x) = (2051+2061+2162+2167+2169+2171+2180+2183+2186+2195+2196+2198+2205+2210+2211)/15 = 2180.6
sample standard deviation (s) = 39
standard error of the mean (SEM) = s/√n = 39/√15 ≈ 10.077
t-score for a 98% confidence level and 14 degrees of freedom (from t-distribution table or calculator) = 2.977
Margin of error (ME) = t-score × SEM = 2.977 × 10.077 ≈ 30.05
Therefore, the 98% confidence interval for the mean hours worked per year in this state is:
(x- ME, x+ ME) = (2180.6 - 30.05, 2180.6 + 30.05) = (2150, 2211)
Rounding to the nearest integer and putting the limits in ascending order, we get:
(2150, 2211)
Visit here to learn more about confidence level brainly.com/question/22851322
#SPJ11
kayla thought of a number, added 4, multiplied by 3, subtracted 5, and got 28 as her final result. what number did she start with?
Answers
Answer:
21
Step-by-step explanation
find the square root of -√1600
Answers
Answer: 400
Step-by-step explanation:
Simplify this expression.
2V5(13 +V2)
Answers
Answer:
26V^5+2V^7
Step-by-step explanation:
40
50
70
100
In the diagram of AABC below, AB AC. The
measure of ZB is 40°.
B
What is the measure of ZA?
X

Answers
The value of angle A is 100⁰.
option D is the correct answer.
What is the measure of angle A?
The measure of angle A is calculated by applying the following formula as shown below;
If line AB is similar to line AC, then angle B must be equal to angle C.
∠ B = ∠ C = 40 ⁰
The value of angle A is calculated as follows;
∠ A = 180⁰ - ( ∠ B + ∠ C ) ( sum of angles in a triangle )
∠ A = 180⁰ - ( 40⁰ + 40⁰ )
∠ A = 180⁰ - ( 80 ⁰ )
∠ A = 100⁰
Learn more about angles in a triangle here: https://brainly.com/question/25215131
#SPJ1
Find the slope of the line through each pair of points.
11) (-20, -4), (-12, -10)
Answers
Answer:
slope= -6/8 or -3/4
Step-by-step explanation:
(-10-(-4)/(-12-(-20)= -6/8
In ΔEFG, g = 34 inches, e = 72 inches and ∠F=21°. Find the area of ΔEFG, to the nearest square inch.
Answers
The area of triangle EFG, to the nearest square inch, is approximately 1061 square inches.
To find the area of triangle EFG, we can use the formula:
\(Area = (1/2) \times base \times height\)
In this case, the base of the triangle is FG, and the height is the perpendicular distance from vertex E to side FG.
First, let's find the length of FG. We can use the law of cosines:
FG² = EF² + EG² - 2 * EF * EG * cos(∠F)
EF = 72 inches
EG = 34 inches
∠F = 21°
Plugging these values into the equation:
FG² = 72² + 34² - 2 * 72 * 34 * cos(21°)
Solving for FG, we get:
FG ≈ 83.02 inches
Next, we need to find the height. We can use the formula:
height = \(EF \times sin( \angle F)\)
Plugging in the values:
height = 72 * sin(21°)
height ≈ 25.52 inches
Now we can calculate the area:
\(Area = (1/2) \times FG \times height\\Area = (1/2)\times 83.02 \times 25.52\)
Area ≈ 1060.78 square inches
For more such questions on triangle
https://brainly.com/question/1058720
#SPJ8
Find the slope of (12, 11) and (-9, 11)
Answers
Answer:
Slope(M)=0
Step-by-step explanation:
Slope(M)=0
Felix joins a local recreation center to play basketball.The recreation center charges a $20 annual fee, plus an additional $15 per month for usage of the basketball courts.Felix prepays by writing a check for $185. For how many months did Felix prepay?
Answers
Answer:
11 months
Step-by-step explanation:
185 - 20 = 165
165 ÷ 15 = 11
A tree grew from 6 feet to 12 feet in one year. What is the percent of change?
Answers
Answer:
100%
Step-by-step explanation:
It doubles in height, which makes it 100%
Answer:
100%
Step-by-step explanation:
The tree grew from 6 feet to 12 feet, which is a growth of 6 feet. 6 feet/6feet is 1, which in percent is 100%.
Now, you could say as the tree doubled in size, the change is 200%, however you must subtract the original height to gain the amount of change. So, 12-6 = 6, and 6/6 = 1, 1*100 = 100%.
Algebra 2 - Grade 11
Can anyone please help me soon as possible?
Use synthetic substitution to find f(–3) and f(4) for each function.
f(x) = x^2 – 5x + 10
f(x) = x^3 + 3x^2 + 2x – 50
Answers
Answer:
for the first equation
f(-3) = 34
f(4) = 6
for the 2nd equation
f(-3) = -56
f(4) ÷ 70
Step-by-step explanation:
my work is attached in a picture.
all you do is substitute each x value into each equation
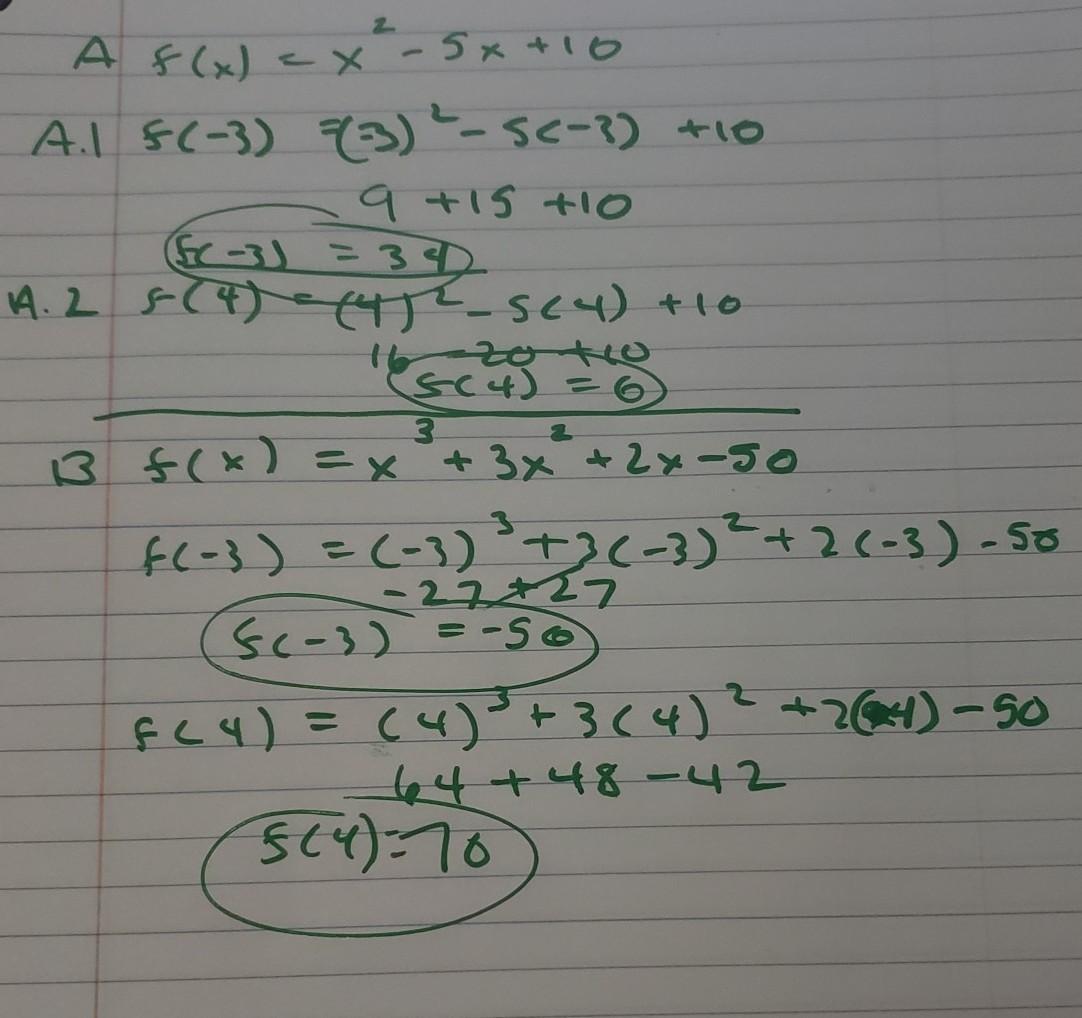
A woman wants to measure the height of a nearby building she places a 10 foot pole in the shadow of the building so that the shadow of the pool is exactly covered by the shadow of the building the total length of the building shadow is 200 feet and the pool cast a shadow that is 5.5 feet long how tall is the building round your answer to the nearest foot
Answers
The height of the building is about 364 feet.
Let's use a proportion to solve the problem. We know that the height of the building and the length of its shadow are proportional to the height of the pole and the length of its shadow. That is:
height of building/length of building shadow = height of pole/length pole shadow
We are given that the height of the pole is 10 feet, and its shadow is 5.5 feet long. We are also given that the length of the building shadow is 200 feet. We don't know the height of the building, so we'll use "h" to represent it. Substituting the given values into the proportion, we get:
h / 200 = 10 / 5.5
We can solve for "h" by cross-multiplying:
h = 200 * 10 / 5.5
h ≈ 363.6
Therefore, the height of the building is approximately 363.6 feet. Rounding to the nearest foot gives us the final answer:
The height of the building is about 364 feet.
To learn more about proportion:
brainly.com/question/29774220
#SPJ4
Use place value to explain each step in finding
3 x 2,746
Answers
The value of the given expression 3 x 2,746 is 8,238.
We are given the expression:-
3 x 2,746
We have to find the value of the given expression using place value.
According to the data given in the question, we can write,
In 2746,
The place value of 6 is 6
The place value of 4 is 4*10 = 40
The place value of 7 is 7*100 = 700
The place value of 2 is 2*1000 = 2000
Hence, we can write,
3*2746 = 3*2000 + 3*700 + 3*40 + 3*6 = 6000 + 2100 + 120 + 18 = 8,238.
To learn more about place value, here:-
https://brainly.com/question/27734142
#SPJ1
Please hurry and help me :)
Greatly appreciate it please.

Answers
Answer:
The center is (4, 7), and the radius is 3.
\( {(x - 4)}^{2} + {(y - 7)}^{2} = 9\)
Brendan lives 2 miles closer to the
library than Jamal does. Jamal lives 1 mile farther from the
library than Aisha does. Jamal lives 3 miles from the library.
How much closer to the library is Brendan than Aisha?
Answers
Answer:
1 mile
Step-by-step explanation:
Jamal's Distance = 3 miles
Since Brendan lives 2 miles closer than Jamal, you do 3 - 2 = 1
Since Jamal lives 1 mile closer than Aisha, you do 3 - 1 = 2
Then, you do 2 - 1
Answer: 1
16-2t=3/2t+9
Solve for t
Answers
Answer:
t=2
Step-by-step explanation:
16-2t=3/2t+9
you multiply everything with 2
32-4t = 3t+18
4t-3t=18-32
-7t=-14
t=2
Step 1: Minus the 16 from the 9
Step2: Multiply the 2t wirh the -2t.
Step 3: Divide -4 by -4

5.13 website registration. a website is trying to increase registration for first-time visitors, exposing 1% of these visitors to a new site design. of 752 randomly sampled visitors over a month who saw the new design, 64 registered. (a) check any conditions required for constructing a confidence interval. (b) compute the standard error. (c) construct and interpret a 90% confidence interval for the fraction of first-time visitors of the site who would register under the new design (assuming stable behaviors by new visitors over time).
Answers
We can use a normal distribution to model phat and construct a confidence interval. We are 90% confident that 6.85% to 10.15% of first-time site visitors will register using the new design.
(a) The visitors are from a simple random sample, so independence is satisfied. The success/failure condition is also satisfied, with both 64 and 752 − 64 = 688 above 10. Therefore, we can use a normal distribution to model phat and construct a confidence interval.
(b) The sample proportion is phat = 0.085, SE = 0.010
(c) For a 90% confidence interval, use z⋆ = 1.65. The confidence interval is 0.085 ± 1.65 × 0.010 → (0.0685, 0.1015). We are 90% confident that 6.85% to 10.15% of first-time site visitors will register using the new design.
Normal distribution is a statistical concept that describes the probability distribution of a random variable that is continuous and symmetric around its mean. It is also known as Gaussian distribution or bell curve because of its characteristic bell-shaped curve. The normal distribution is important in statistical analysis because it occurs naturally in many real-world situations, such as the distribution of heights, weights, and test scores. It is also used in hypothesis testing and in the construction of confidence intervals.
The normal distribution is characterized by two parameters: the mean, which is the central tendency of the distribution, and the standard deviation, which measures the spread or dispersion of the distribution. The standard deviation determines the width of the bell curve, with a larger standard deviation indicating a wider curve.
To learn more about Normal distribution visit here:
brainly.com/question/17199694
#SPJ4
Identify the leading coefficient in the following polynomial:
10x2 + 3x – 5
Answers
Answer:
The leading coefficient in the polynomial 10x2 + 3x - 5 is 10.
Step-by-step explanation:
To find the leading coefficient of the polynomial function, we must first locate the leading term. In a polynomial function, the leading term is the term containing the highest power of x. In this polynomial function, the leading term is 10x2. The leading coefficient of a polynomial function is the coefficient of the leading term, and so the leading coefficient of this polynomial function is 10.
Working together, 6 friends picked 18 and (1/2) dozen of various apples. They divided the apples equally among themselves. How many apples does each person get? Each person will get 3 and (1/12) apples.
Answers
Answer:its c
Step-by-step explanation: hope this helped have a good day or night :)
i need help with this question thanks :)
the options are
45
33.75
50
not here

Answers
Answer:
UV = 45
Step-by-step explanation:
ZY is the perpendicular bisector of UV , then
UV = 2 × UY = 2 × 22.5 = 45
-18 ≥ 4 + 2q
Solve for me, please.
Answers
Answer
q≤ -11
thats your answer i believe, just typing this because it said it was too short to post
Write an explicit rule for the recursive rule. a1=8,
an=an−1−12
Answers
Answer:
\(a_{n}\) = 20 - 12n
Step-by-step explanation:
the explicit rule for an arithmetic sequence is
\(a_{n}\) = a₁ + (n - 1)d
where a₁ is the first term and d the common difference
a recursive rule has the form
\(a_{n}\) = \(a_{n-1}\) + d
given recursive rule
\(a_{n}\) = \(a_{n-1}\) - 12 : a₁ = 8
then a₁ = 8 and d = - 12
explicit rule is therefore
\(a_{n}\) = 8 - 12(n - 1) = 8 - 12n + 12 = 20 - 12n
PLEASEEEE HELPPPPP A flying disk is thrown into the air from a height of 25 feet at time t=0. The function that models this situation is h(t) = -16t2 + 75t + 25, where t is measured in seconds and h is the height in feet. Which values best describe the domain of the function in the context of the problem?
A. 0 ≤ t ≤ 5
B. 0 ≤ t ≤ 25
C. All real numbers
D. All positive integers
Answers
Answer:
A)
Step-by-step explanation:
Given function:
\(h(t)=-16t^2+75t+25\)
The domain (input values) will be the x-intercepts, so the values of t when h(t) = 0.
The quickest way to find these is to use the quadratic formula.
Quadratic Formula
\(x=\dfrac{-b \pm \sqrt{b^2-4ac} }{2a}\quad\textsf{when}\:ax^2+bx+c=0\)
\(\implies t=\dfrac{-75 \pm \sqrt{75^2-4(-16)(25)} }{2(-16)}\)
\(\implies t=\dfrac{-75 \pm \sqrt{7225}}{-32}\)
\(\implies t=\dfrac{75 \pm 85}{32}\)
\(\implies t=5, t=-\dfrac{5}{16}\)
Time cannot be negative.
When h(t) = 0, the disk will hit the floor.
Therefore, the domain is restricted to 0 ≤ t ≤ 5
What is 100 x (81 + 283) - 67 x 4
Answers
Answer: 36132
Step-by-step explanation:
81+283=364
100*364=36400
67*4=268
36400-268=36132
Answer:
Step-by-step explanation:
100*(81+283)-67*5
=36400-268
=36132
what is the value of a²+ab+b² when a =0 and b=-1?
Answers
Step-by-step explanation:
a²+ab+b²
(0)^2 + (0)(1) + (1^2)
0 + 0 + 1 = 1
(9h+3)(−h−1) porfavor ayudenme con esta pregunta.
Answers
Answer:
-9h² - 12h - 3
Step-by-step explanation:
Follow the FOIL method:
FOIL = First, Outside, Inside, Last
Multiply the terms together:
First: 9h * -h = -9h²
Outside: 9h * -1 = -9h
Inside: 3 * -h = -3h
Last: 3 * -1 = -3
Combine like terms: 9h² + (-9h - 3h) - 3
9h² - 12h - 3
-9h² - 12h - 3 is your answer.
~
-9h^2 - 9h -3h -3 = 0
-9h^2 -12h -3 = 0
(h+1)(3h+1) = 0
h = -1, h = -1/3
Has the marrying age of a man changed over the years? The United States Bureau of the Census takes a formal count of everyone in the U.S. every 10 years and has provided the following data that gives the median age of an American man at the time of his first marriage.
Year
1910
1920
1930
1940
1950
1960
1970
1980
1990
2000
Median Age
25.1
24.6
24.3
24.3
22.8
22.8
23.2
24.7
26.1
26.8
Determine the average rate of change in median age per year from 1930 to 1960.
a.
-0.5 years of age per year
b.
20 years of age per year
c.
-0.05 years of age per year
d.
+0.05 years of age per year
Answers
-0.05 is the average rate of change in median age per year from 1930 to 1960.
What is ratio?The ratio can be defined as the number that can be used to represent one quantity as a percentage of another. Only when the two numbers in a ratio have the same unit can they be compared. Ratios are used to compare two objects.
Given, a data set that gives the median age of an American man at the time of his first marriage.
Year Median age
1910 25.1
1920 24.6
1930 24.3
1940 24.3
1950 22.8
1960 22.8
1970 23.2
1980 24.7
1990 26.1
2000 26.8
The average rate of change from 1930 to 1960 = (-24.3 + 22.8) / (1960-1930)
The average rate of change from 1930 to 1960 = -0.05
Therefore, the average rate of change in median age per year from 1930 to 1960 is -0.05.
Learn more about ratios here:
https://brainly.com/question/13419413
#SPJ1
A boat traveling for 6 hours with the current goes 20 more miles than it travels in 10 hours against the current. What is the speed of the current if the speed of the boat in still water is 15mph ?
Answers
The speed of the current is 5 mph.
Let the speed of the current be x mph.Speed of the boat downstream = (Speed of the boat in still water) + (Speed of the current)= 15 + x.Speed of the boat upstream = (Speed of the boat in still water) - (Speed of the current)= 15 - x.
Let us assume the distance between two places be d .According to the question,20 = (15 + x) × 6 - d (1)
Distance covered upstream in 10 hours = d. Distance covered downstream in 6 hours = d + 20.
We know that time = Distance/Speed⇒ Distance = Time × Speed.
According to the question,d = 10 × (15 - x) (2)⇒ d = 150 - 10x (2)
Also,d + 20 = 6 × (15 + x)⇒ d + 20 = 90 + 6x⇒ d = 70 + 6x (3)
From equation (2) and equation (3),150 - 10x = 70 + 6x⇒ 16x = 80⇒ x = 5.
for such more question on speed
https://brainly.com/question/13943409
#SPJ8
The lengths of the sides of a right angled triangle are ( x+1)cm,4x cm,and (4x+1) cm . Find the value of x
Answers
Answer:
The value of x is 6.
Step-by-step explanation:
You have to use Pythagorean Theorem, a² + b² = c². Make (4x+1)cm as the hypotenuse because any values substitute into x will give the highest length among these 3 expressions of length :
\( {a}^{2} + {b}^{2} = {c}^{2} \)
Let a = side = (x+1)cm,
Let b = side = 4x cm,
Let c = hypotenuse = (4x+1)cm,
\( {(x + 1)}^{2} + {(4x)}^{2} = {(4x + 1)}^{2} \)
\( {x}^{2} + 2x + 1 + 16 {x}^{2} = 16 {x}^{2} + 8x + 1\)
Then you have to simplify :
\(17 {x}^{2} + 2x + 1 = 16 {x}^{2} + 8x + 1\)
\(17{x}^{2} + 2x + 1 - 16 {x}^{2} - 8x - 1 = 0\)
\( {x}^{2} - 6x = 0\)
Next you have to solve it :
\( {x}^{2} - 6x = 0\)
\(x(x - 6) = 0\)
\(x = 0 \: (rejected)\)
\(x - 6 = 0\)
\(x = 6cm\)
The value of x in the right triangle is 6 cm.
What is the Pythagorean theorem?Pythagorean theorem states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
We have,
Right triangle:
The three sides are:
x + 1, 4x and 4x + 1
Applying the Pythagorean theorem.
(x + 1)² + (4x)² = (4x + 1)²
x² + 2x + 1 + 16x² = 16x² + 8x + 1
17x² + 2x + 1 = 16x² + 8x + 1
17x² - 16x² = 8x - 2x
x² = 6x
x gets canceled.
x = 6
Thus,
The value of x is 6.
Learn more about the Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ2
Point P has coordinates (3, -4). If P is reflected across the x-axis, what are the coordinates of the P'
Answers
In response to the query, we can state that Hence, P"s coordinates are coordinates (3, 4).
what are coordinates?When locating points or other geometrical objects precisely on a manifold, such as Euclidean space, a coordinate system is a technique that uses one or more integers or coordinates. Locating a point or item on a two-dimensional plane requires the use of coordinates, which are pairs of integers. Two numbers called the x and y coordinates are used to describe a point's location on a 2D plane. a collection of integers that represent specific locations. The figure often has two numbers. The first number denotes the front-to-back measurement, while the second number denotes the top-to-bottom measurement. For example, in (12.5), there are 12 units below and 5 above.
A point's y-coordinate changes sign when it is reflected across the x-axis, but its x-coordinate stays the same.
Hence, we must modify the sign of the y-coordinate while leaving the x-coordinate unaffected in order to reflect point P(3,-4) across the x-axis. The reflected point P' will therefore have coordinates (3, 4).
Hence, P"s coordinates are (3, 4).
To know more about coordinates visit:
https://brainly.com/question/27749090
#SPJ1