What is the general solution to the differential equation dy over dx equals x times y plus 2 times x
Answers
The general solution to the given differential equation, \(\frac{dy}{dx}\) = x × y + 2 × x, can be found by separating the variables and integrating.
Step 1:
Rearrange the equation to separate the variables:
dy = (x × y + 2 × x) dx
Step 2:
Divide both sides by (y + 2x):
\(\frac{dy}{y + 2x}\) = x dx
Step 3:
Integrate both sides of the equation:
∫(\(\frac{1}{y + 2x}\))) dy = ∫x dx
Step 4:
Solve the integrals separately:
ln|y + 2x| = (\(\frac{1}{2}\)) × x² + C1
Step 5:
Remove the natural logarithm by taking the exponential of both sides:
|y + 2x| =\(e^{\frac{1}{2} }\) × x² + C1)
Step 6:
Consider two cases: positive and negative values of (y + 2x).
Case 1:
(y + 2x) > 0
y + 2x
= \(e^{\frac{1}{2} }\) × x² + C1)
Case 2:
(y + 2x) < 0
-(y + 2x)
= \(e^{\frac{1}{2}}\) × x² + C1
Step 7:
Simplify the equations:
y = -2x + \(e^{\frac{1}{2} }\) × x² + C1) (for (y + 2x) > 0)
y = -2x - \(e^{\frac{1}{2} }\) × x² + C1) (for (y + 2x) < 0)
These are the general solutions to the given differential equation.
They describe all possible solutions in terms of an arbitrary constant, C1.
To know more about equation visit:
https://brainly.com/question/29657983
#SPJ11
The general solution to the given differential equation is \(y = Ke^{x^2}\), where K is a non-zero constant. This solution represents a family of curves that satisfy the given differential equation.
The general solution to the differential equation \(\frac{dy}{dx} = xy + 2x\) can be found using the method of separable variables. Here's how you can solve it:
1. Rewrite the equation:
\(\frac{dy}{dx} = xy + 2x\)
2. Separate the variables by moving all terms involving y to one side and terms involving x to the other side:
\(\frac{dy}{y} = 2xdx.\)
3. Integrate both sides separately:
\(\int(\frac{dy}{y}) = \int2xdx.\)
4. Integrate the left side by applying the natural logarithm property:
\(ln|y| = x^2 + C_1\)
where:
\(C_1\) is the constant of integration.
5. Integrate the right side:
\(\int 2xdx = x^2 + C_2\)
where:
\(C_2\) is another constant of integration.
6. Combine the integration results:
\(ln|y| = x^2 + C_1 + C_2\)
7. Rewrite the equation using properties of logarithms:
\(ln|y| = x^2 + C\)
8. Solve for y by taking the exponential of both sides:
\(|y| = e^{(x^2+C)}\)
9. Remove the absolute value by considering two cases:
\(y = \pm e^{(x^2+C)}\)
10. Simplify the expression:
\(y = Ke^{x^2}\)
where K is a non-zero constant.
In conclusion, the general solution to the given differential equation is \(y = Ke^{x^2}\), where K is a non-zero constant. This solution represents a family of curves that satisfy the given differential equation.
Learn more about differential equation from the given link:
https://brainly.com/question/1164377
#SPJ11
Related Questions
What is one fifth of 13.7?
Answers
Answer:
2.74
Step-by-step explanation:
Answer: 2.74
Step-by-step explanation: When it says 1/5 of this number, you just divide it by the denominator (5) So, 13.7 / 5 = 2.74. To check, we multiply 2.74 by the denominator. (5) We get 13.7. This makes the statement true. I hope this helped!
28. From the four numbers below, Maria chose one number. The number is even and none of its digits are the same. The hundreds digit is triple the ones digit. The tens digit is greater than the thousands digit. Which number did Maria choose? A. 3672 B. 4983 C. 2682 D. 8462
Answers
Answer:
Maria chose C. 2682
Step-by-step explanation:
Andrew spent 75% of his $20 allowance to go to the movies. How much did he spend? Use at least 2 strategies.
PLEASE HELP
Answers
Answer:
$15
Step-by-step explanation:
Which graph represents the solution to the system of equations?
Y=2x+5. Y=1/3x-2
Please help me

Answers
Answer:
I can help but I need better pic
What is the value of the expression?

Answers
Answer:
C
Step-by-step explanation:
Substitute the given values into the expression
\(\frac{v}{2}\) + (\(\frac{3}{4}\) - w )
= \(\frac{1}{2}\) + (\(\frac{3}{4}\) - \(\frac{5}{8}\) ) ← evaluate parenthesis
= \(\frac{1}{2}\) + (\(\frac{6}{8}\) - \(\frac{5}{8}\) )
= \(\frac{1}{2}\) + \(\frac{1}{8}\)
= \(\frac{4}{8}\) + \(\frac{1}{8}\)
= \(\frac{5}{8}\)
Calculate net force:
Question 4 options:
17 N
3 N
70 N
none of the above

Answers
Answer:
3N
Step-by-step explanation:
The graph states that the forces are acting in opposite directions, so subtract the value of the smaller force from the larger to find net force.
Hope this helps!
Use the function below (whose parameters qualify it as a STC function) to answer the questions.
"STC "=" 6 "+"9 Q - 3" "Q" ^2 +" (1/3)" "Q" ^3
a) Total fixed cost is $_________
b) Obtain the AFC function from (a) and write it here __________________
c) Obtain the AVC function contained in the STC function and write the AVC function here _________________________
d) Write here the MC function __________________________
e) Find the value which AFC approaches as Q gets very large. Also write a sentence or two explaining what this implies for fixed costs per unit (AFC) as production quantities get ever larger.
f) Find the value of Q at which AVC is a minimum.
g) Is productive efficiency at the value in (f) greatest or least?
h) Demonstrate that the value of SMC equals the value of AVC at the value of Q where AVC is a minimum. Hint: The level of Q you found in (f) is where AVC is a minimum. If you plug this level of Q into AVC (see c) and also into MC (see d) the two outcomes should be the same if SMC crosses AVC at this level of Q.
i) Why does the derivative of Short Run Total Cost (STC) equal the derivative of Total Variable Cost (TVC)? Stated another way, why does dSTC/dQ = dTVC/dQ? Explain in a couple of sentences.
j. Find the value of Q where increasing returns ceases and diminishing returns begins. Hint: Diminishing returns begins at the level of Q where MC is a minimum
Answers
Total fixed cost is $6. The value of AFC is $6 / Q. Productive efficiency is greatest at Q = 4.5. Diminishing returns begin when Q = 3. The total fixed cost (TFC) does not change because it is fixed.
a) Total fixed cost is $6
b) We can obtain the average fixed cost function (AFC) from the total fixed cost (TFC) by dividing it by output (Q) as follows: AFC = TFC / Q. So, the value of AFC is $6 / Q.
c) The AVC function is calculated by dividing total variable cost (TVC) by output (Q).
STC = TFC + TVC6 + 9Q - 3Q2 + (1/3)Q3TVC = 9Q - 3Q2 + (1/3)Q3AVC = TVC / QAVC = (9Q - 3Q2 + (1/3)Q3) / QAVC = 9 - 3Q + (1/3)Q2
d) The MC function is derived by taking the first derivative of the STC function with respect to output (Q). The derivative of the STC function is: MC = dSTC / dQMC = 9 - 6Q + Q2
e) As Q approaches infinity, the denominator of AFC becomes larger and larger. So, AFC approaches zero as Q gets very large. This implies that fixed costs per unit decrease as production quantities get larger.
f) We can find the value of Q at which AVC is a minimum by taking the first derivative of the AVC function and setting it equal to zero. The first derivative of AVC is: AVC = 9 - 3Q + (1/3)Q2
dAVC / dQ = -3 + (2/3)Q= 0
Q = 4.5
g) Productive efficiency is greatest when AVC is at its minimum. Therefore, productive efficiency is greatest at Q = 4.5.
h) We can demonstrate that the value of SMC equals the value of AVC at the value of Q where AVC is a minimum by plugging Q = 4.5 into both the AVC and MC functions. AVC = 9 - 3(4.5) + (1/3)(4.5)2AVC = 7.125MC = 9 - 6(4.5) + 4.52MC = 7.125
Since SMC = MC, we can conclude that SMC equals AVC at the value of Q where AVC is a minimum.
i) In the short run, the total fixed cost (TFC) does not change because it is fixed. Therefore, the derivative of the STC function with respect to output (Q) is equal to the derivative of the TVC function with respect to output (Q). This means that dSTC / dQ = dTVC / dQ.
j) Increasing returns to scale cease when the marginal cost (MC) is equal to average total cost (ATC). Diminishing returns to scale begins when MC exceeds ATC. ATC is calculated by dividing the total cost (TC) by output (Q). TC is calculated by adding total fixed cost (TFC) and total variable cost (TVC).
ATC = TC / QATC = (6 + 9Q - 3Q2 + (1/3)Q3) / Q
Now, we can find the level of Q where increasing returns to scale cease by calculating the first derivative of ATC and setting it equal to zero.
ATC = (6 + 9Q - 3Q2 + (1/3)Q3) / QdATC / dQ = (6 - 6Q + Q2) / Q2= 0
Q = 3
Now, we can calculate the marginal cost function and find the level of Q where diminishing returns begins. We know that diminishing returns begin where the marginal cost is at its minimum.
MC = 9 - 6Q + Q2MC = 9 - 6(3) + 32MC = 3
So, diminishing returns begin when Q = 3.
To know more about total fixed cost, visit:
https://brainly.com/question/30826886
#SPJ11
The triangles below are similar. Triangle A has a side lengths with the measure 3m,5m, and 4m. Triangle b has side lengths with the measure 12m, 20m, and x
Find the value of x
Answers
Answer:
x=16
Step-by-step explanation:
You multiply 4 by 4 because when you multiply 3by 4 you get 12, when you multiply 5by 4 you get twenty and since they are similar triangles you have to multiply 4 by 4
PLS HELP WILL MARK U BRAINLIEST!! NO FAKE ANSWERS

Answers
Answer:
C
Step-by-step explanation:
C is not true
You toss a coin, what is the probability of having 5 heads in a row? 1/64 O 1/8 O 1/4 O 1/32 O 1/16
Answers
Answer:
Step-by-step explanation:
The Probability of Landing a heads is (1/2)
Now, to find the probability of landing it five times in a row, it is
1/2 x 1/2 x 1/2 x 1/2 x 1/2
( 1/2 is multiplied to the number of times to get a head )
The final answer will be,
Probability of landing heads 5 times in a row = 1/32
Braden salazar was deployed in a combat zone for all of 2021. He is married and has two children. Braden's nontaxable combat pay in 2021 is $14,000. His wife worked part-time while braden was deployed and earned $7,000. What is the maximum amount of earned income the salazars can report for eitc purposes in 2021?.
Answers
The amount of earned income the Salazars can report for EITC purposes in 2021 is $21,000.
The maximum amount of earned income the Salazars can report for EITC purposes in 2021 is $21,000. This is calculated by adding Braden's nontaxable combat pay ($14,000) and his wife's earned income ($7,000).
Formula:
Maximum Earned Income for EITC = Braden's Nontaxable Combat Pay + Wife's Earned Income
Maximum Earned Income for EITC = $14,000 + $7,000
Maximum Earned Income for EITC = $21,000
Learn more about Amount here :
https://brainly.com/question/28970975
#SPJ4
christina's pizza sells pizza by the slice for lunch. today, they sold 76 slices, including 20 slices of pepperoni pizza. what is the experimental probability that the first slice sold during lunch tomorrow will be a slice of pepperoni pizza?
Answers
The experimental probability that the first slice sold during lunch tomorrow will be a slice of pepperoni pizza is approximately 0.263
The experimental probability is found by dividing the number of times the desired outcome occurred by the total number of trials. In this case, the desired outcome is selling a slice of pepperoni pizza as the first slice tomorrow.
Since we only know the number of slices sold today, we don't have any specific information about the number of slices that will be sold tomorrow. However, we can assume that the same types of pizzas will be sold tomorrow, and the probability of selling a slice of pepperoni pizza tomorrow will be the same as the proportion of pepperoni slices sold today.
So, the experimental probability that the first slice sold during lunch tomorrow will be a slice of pepperoni pizza is
Experimental probability = Number of pepperoni slices sold today / Total number of slices sold today
Experimental probability = 20 / 76
Experimental probability = 0.263
Learn more about Experimental probability here
brainly.com/question/30694293
#SPJ4
which of the following is a quadratic equation :
\(x + 1 \x = x ^{2} \)
x2 + 1/x2 = 5
x2 + 3rootx + 7 = 0
2x2 - 5x = (x-1)2
Answers
Answer:
a, b and c are not polynomial
and d I'd correct
2x² - 5x = x² -2x +1
A jacket is reduced from $20 to $14. By what percentage was the price of the jacket reduced?
Answers
Answer: 30%
Step-by-step explanation:
20-14=6
this is the amount reduced
6/20 multiply this by 100, which is 600/20, which equals 30%
Hope this helps!
describe a set of transformations that would map red triangle to the blue triangle
Answers
A set of transformations that would map red triangle to the blue triangle is rotate 90° clockwise and then translate 6 units down (option a).
Let us consider two triangles, A and B. We are given four transformations, and we need to determine which one maps triangle A to triangle B. To do this, we need to understand the effect of each transformation on the position, orientation, or size of the triangle.
Transformation A involves rotating triangle A by 90 degrees clockwise and then translating it 6 units down.
A rotation is a transformation that preserves the shape and size of a triangle but changes its orientation. In this case, the rotation is 90 degrees clockwise, which means that each vertex of triangle A is rotated 90 degrees in a clockwise direction about the origin.
After the rotation, the triangle is translated 6 units down, which means that each vertex is shifted 6 units downward. If we apply transformation A to triangle A, we obtain a new triangle that has the same shape and size as triangle A, but its position and orientation are different.
This new triangle is similar to triangle B if its corresponding angles are congruent and its corresponding sides are proportional.
Hence the correct option is (a).
To know more about triangle here
https://brainly.com/question/8587906
#SPJ4
Complete Question:
Describe the transformations that will map triangle A to triangle B and illustrate the similarity between the two triangles.
A) rotate 90° clockwise and then translate 6 units down
B) translate 4 units down and rotate 180° about the origin
C) reflect the triangle across the y-axis and translate 4 units down
D) reflect triangle A across the x-axis and then translate 1 unit right

pls help!!!!!!!!!!!!

Answers
Answer:116
angles in a triangle is 180.
Answer:
1=116
2=32
Thank You
Find the slope of the tangent line to f(x)=6sin(x) at x=π/6
Answers
The required slope of the tangent line to f(x) = 6 sin(x) at x = π/6 is 3 √3.
What is slope?The value of the steepness or the direction of a line in a coordinate plane is known as the slope of a line, often known as the gradient. Given the equation of a line or the coordinates of points situated on the straight line, slope can be determined using a variety of techniques.
The formula for slope between two points (x₁, y₁) and (x₂, y₂) is,
m = (y₂ - y₁)/(x₂ - x₁)
The slope is also denoted by tan θ.
The given equation of line,
f(x) = 6 sin(x)
To find the slope of the given line, differentiate with respect to x,
f'(x) = tan θ = d/dx(6 sin(x))
= 6 d/dx(sin(x))
= 6 cos x
At x = π/6, the slope of line,
f'(π/6) = 6 cos(π/6)
= 6 (√3 / 2)
= 3 √3
The slope of the tangent line to f(x) = 6 sin(x) is 3 √3.
To know more about Slope on:
https://brainly.com/question/16941905
#SPJ1
31.3 correct answers. 0.8 incorrect answers overall score 97.7% is this a good score.....?!!!! Plssss
Answers
Answers
yes it ia
Step-by-step explanation:
Prove (f_n) does not converge uniformly using epsilon criteria: for any natural number N, for all n >= N, then | f_n(x) - f(x) | < ε for all x in [0,1] and ε > 0.
I have already proved it converges point-wise to f(x) = 0 when 0 <= x < 1 and f(x) = 1 if x = 1. For n E N, let fn: [0, 1] → R be given by fn(x) = x.
Answers
ε = 1/2 is fixed, we have |fn(x) − f(x)| ≥ ε for all n ≥ N and for some x in [0,1].Therefore, (fn) does not converge uniformly to f(x) on [0,1] using epsilon criteria.
Given that fn: [0, 1] → R is given by fn(x) = x and you have already proved that (fn) converges point-wise to f(x) = 0 when 0 ≤ x < 1 and f(x) = 1 if x = 1.
Now, to prove that (fn) does not converge uniformly using epsilon criteria, we need to negate the definition of uniform convergence. Definition: (fn) converges uniformly to f(x) on [0,1] if, for any ε > 0, there exists a natural number N such that |fn(x) − f(x)| < ε for all n ≥ N and for all x in [0,1].
Negation of Definition: (fn) does not converge uniformly to f(x) on [0,1] if, there exists an ε > 0 such that, for all natural numbers N, there exists an n ≥ N and x in [0,1] such that |fn(x) − f(x)| ≥ ε. Let ε = 1/2 and let N be a natural number. Consider x = min{1, 2/N}. Since N is a natural number, 2/N ≤ 1. So x = 2/N and x is an element of [0,1]. Also, fn(x) = x for all n. Thus, |fn(x) − f(x)| = |x − 0| = x. Note that x can be made arbitrarily small by choosing N large enough.
Since ε = 1/2 is fixed, we have |fn(x) − f(x)| ≥ ε for all n ≥ N and for some x in [0,1].Therefore, (fn) does not converge uniformly to f(x) on [0,1] using epsilon criteria.
to know more about natural number visit :
https://brainly.com/question/2228445
#SPJ11
We have proved that the sequence (fn) does not converge uniformly.
Given that for any natural number N, for all n ≥ N, then |fn(x) - f(x)| < ε for all x in [0,1] and ε > 0.
Let us prove that the sequence (fn) does not converge uniformly.
Let ε = 1/2.
Take any natural number N.
Choose n ≥ N. Consider |fn(1) - f(1)| = |1 - 1| = 0. It is less than ε = 1/2.
Hence, the sequence (fn) is pointwise convergent to the function f(x) = 0 when 0 ≤ x < 1 and f(1) = 1.
Take ε = 1/4. Choose any natural number N.
Then choose n ≥ N.
Consider |fn(1 - 1/n) - f(1 - 1/n)| = |(1 - 1/n) - 0|
= 1 - 1/n.
It is greater than ε = 1/4.
Thus, the sequence (fn) is not uniformly convergent on [0,1].
Therefore, we have proved that the sequence (fn) does not converge uniformly.
To know more about converge uniformly, visit:
https://brainly.com/question/32662733
#SPJ11
the relationship between the amount of time a zebra runs at maximum speed and the distance it covers is shown. write an equation to describe this relationship.
Answers
The equation that describes the relationship between the time a zebra runs at a speed and the distance it covers is y = 2/3(x).
What is the equation of the line?A linear equation is an algebraic equation of the form y=mx+b. where m is the slope and b is the y-intercept.
Assuming that the relationship between the time a zebra runs at a speed and the distance it covers is a linear one, we can use the formula for the equation of a straight line:
y = mx + b
where y is the distance covered, x is the time the zebra runs at a speed, m is the slope (i.e., the speed of the zebra), and b is the y-intercept (i.e., the distance covered when the zebra is not running).
From the table two points can be formed as (x, y) that are, (3, 2) and (6, 4)
Using these two points, we can find the slope of the line:
m = (y₂ - y₁)/(x₂ - x₁)
= (4 - 2)/(6 - 3)
= 2/3
Now as we have the slope m we can use it in point slope form, i.e.
y - y₁ = m(x - x₁)
Using the point (3, 2),
y - 2 = 2/3(x - 3)
y - 2 = 2/3(x) - 2
y = 2/3(x) - 2 + 2
y = 2/3(x)
Hence, the equation that describes the relationship between the time a zebra runs at maximum speed and the distance it covers is:
y = 2/3(x)
To learn more about the equation of line visit:
https://brainly.com/question/18831322
#SPJ1
Complete question:
The relationship between the amount of time a zebra run at maximum speed in the distance it covers is shown.
Write an equation to describe this relationship.

2-simplifica
1)x²-5x-16
x+2=
2)6an²-3b²n²
b4-4ab²+4a²=
3)4x²-4xy+y²
5y-10x
4)n+1-n³-n²
n³-n-2n²+2=
5)17x³y4z6
34x7y8z10=
6)12a²b³
60a³b5x6=
Answers
1. x² - 5x - 16 can be written as (x - 8)(x + 2).
2. 6an² - 3b²n² = n²(6a - 3b²).
3. This expression represents a perfect square trinomial, which can be factored as (2x - y)².
4. Combining like terms, we get -n³ - n² + n + 1 = -(n³ + n² - n - 1).
5. 17x³y⁴z⁶ = (x²y²z³)².
6. 12a²b³ = (2a)(6b³) = 12a6b³ = 12a⁷b³x⁶.
Let's simplify the given expressions:
Simplifying x² - 5x - 16:
To factorize this quadratic expression, we look for two numbers whose product is equal to -16 and whose sum is equal to -5. The numbers are -8 and 2.
Therefore, x² - 5x - 16 can be written as (x - 8)(x + 2).
Simplifying 6an² - 3b²n²:
To simplify this expression, we can factor out the common term n² from both terms:
6an² - 3b²n² = n²(6a - 3b²).
Simplifying 4x² - 4xy + y²:
This expression represents a perfect square trinomial, which can be factored as (2x - y)².
Simplifying n + 1 - n³ - n²:
Rearranging the terms, we have -n³ - n² + n + 1.
Combining like terms, we get -n³ - n² + n + 1 = -(n³ + n² - n - 1).
Simplifying 17x³y⁴z⁶:
To simplify this expression, we can divide each exponent by 2 to simplify it as much as possible:
17x³y⁴z⁶ = (x²y²z³)².
Simplifying 12a²b³:
To simplify this expression, we can multiply the exponents of a and b with the given expression:
12a²b³ = (2a)(6b³) = 12a6b³ = 12a⁷b³x⁶.
Learn more about expression from
https://brainly.com/question/723406
#SPJ11
what is the perimeter of the trapezoid
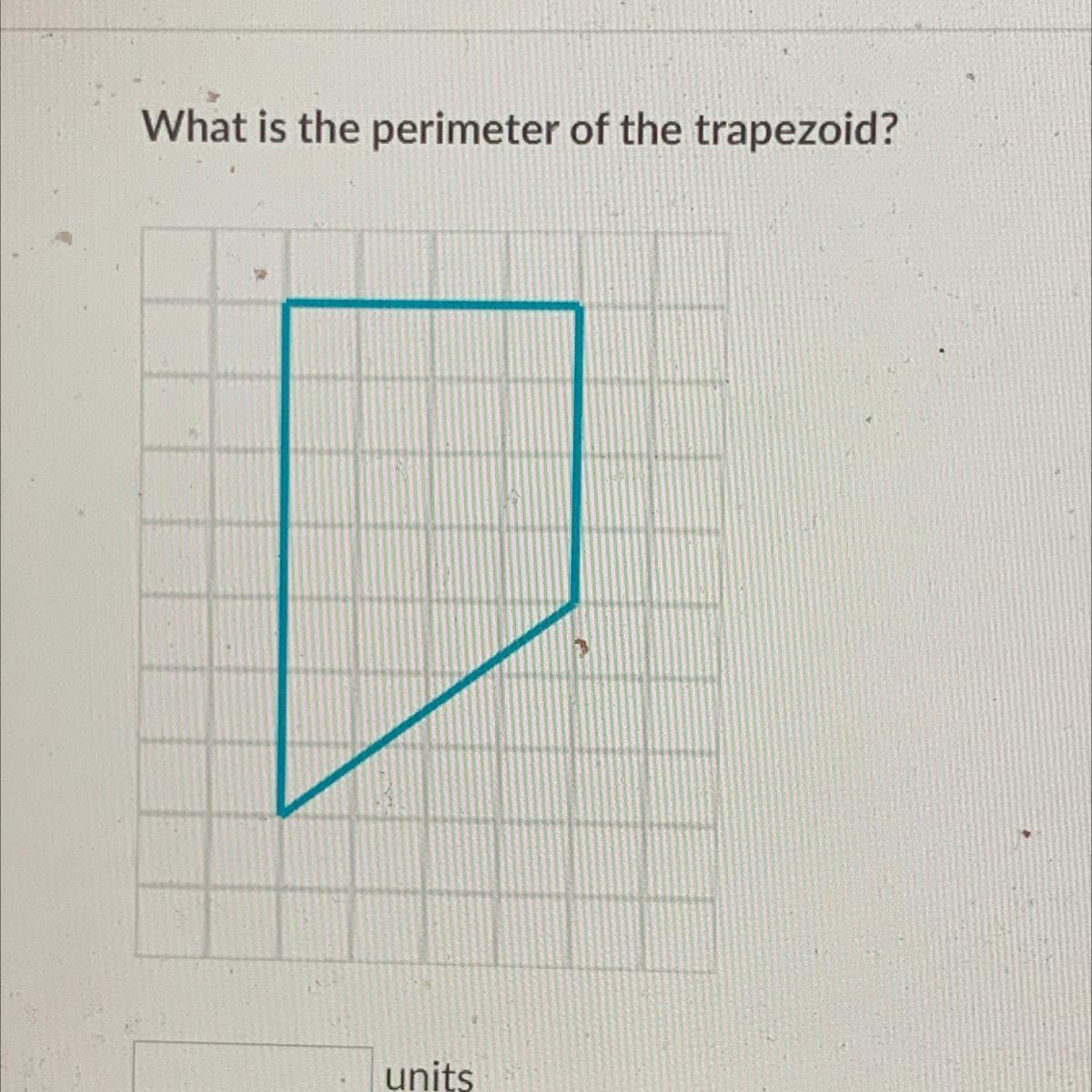
Answers
Answer:
P = a + b + c + d
Step-by-step explanation:
Remember that perimeter is the measure of the outer edge of a shape, or otherwise, the sum of the measures of the sides of the trapezoid. Representing the perimeter by P, and the sides as a, b, c and d, our formula is P = a + b + c + d.
Length of DE is ___
units.
Length of DB is ___
units.
Measure of angle FED is ___
degrees.

Answers
Answer:
Length of DE = 7.5 units
Length of DB = 9.2 units
Measure of ∠FED = 82°
Step-by-step explanation:
In ΔABC,
AD ≅ BD and CE ≅ BE [Given]
By the theorem of mid-segments,
DE = \(\frac{1}{2}(AC)\)
= \(\frac{1}{2}(15)\)
DE = 7.5 units
Since AD ≅ FE ≅ 9.2 [By midpoint theorem in ΔACB]
Therefore, length of DB = 9.2 units
[Although it's not given in the question, but we assume FE║AB]
Since FE║AB and DE is a transverse,
Therefore, m(∠FED) ≅ m(∠BDE) ≅ 82° [Interior alternate angles]
if you roll a dice one time what is the probability for it not to land on an odd number
Answers
Answer:
3/6
Step-by-step explanation:
Simple-
One di has 6 sides.
Three sides are even numbers
We are looking for the probability of not having and odd number chosen
It would be 3/6 because there are 3 even numbers and 3 odd numbers, and we are using even numbers because we need to know the probability of not landing on an odd number.
Hope this helps!!!!
:)
Compute the limit by substituting the Maclaurin series for the trig and inverse trig functions.
(Use symbolic notation and fractions where needed.)
lim x → 0 tan^− 1 ( 4x ) − 4xcos(4x ) − 32/3(x^3)/ (x^5) =
Answers
To substitute the Maclaurin series for the trig and inverse trig functions. The Maclaurin series for tangent inverse is:
tan^−1(x) = x - x^3/3 + x^5/5 - x^7/7 + ...
Similarly, the Maclaurin series for cosine is:
cos(x) = 1 - x^2/2 + x^4/24 - x^6/720 + ...
Substituting these series into the limit expression, we get:
lim x → 0 [tan^−1(4x) - 4xcos(4x) - 32/3(x^3)]/ (x^5)
= lim x → 0 [(4x - (4x)^3/3 + (4x)^5/5 - (4x)^7/7 + ...) - 4x(1 - (4x)^2/2 + (4x)^4/24 - (4x)^6/720 + ...) - 32/3(x^3)]/ (x^5)
= lim x → 0 [-32/3 + 128x^2/15 - ...]/ x^2
= -32/3
Therefore, the limit by substituting the Maclaurin series for the trig and inverse trig functions is -32/3.
To know more about series visit :-
https://brainly.com/question/15692483
#SPJ11
My question is, on Sunday, 77,098 fans attended a New York Jets game. The same day, 3,397 more fans attended a New York Giants game than attended the Jets game. Altogether, how many fans attended the games? Round each number to the nearest thousand to find an estimate of how many fans attended the games.
Answers
Answer:
Total number of fan = 80,495
Step-by-step explanation:
Given:
Number of fans attended = 77,098
Additional number of fans attended = 3,397
Find:
Total number of fan
Computation:
Total number of fan = Number of fans attended + Additional number of fans attended
Total number of fan = 77,098 + 3,397
Total number of fan = 80,495
What property is this?(n+13) + 4 = n + (13+4) Associative Property Commutative Property Additive Identity O Distributive Property
Answers
Answer:associative property?
Step-by-step explanation: because you adding
Whch of the binomials below is a factor of this trinomial x^2 + 19x + 84.
A)x-7
B)x^2+12
C)x+84
D)x+7
Answers
Answer:
The answer is D) x+7
Step-by-step explanation:
First you have to find multiples of 84 and see if they add up to equal 19.
If M=1,000,P=2.25, and Y=2,000, what is velocity? a. 2.25 b. 4.5 c. 2 d. None of the above is true
Answers
Answer:d
Step-by-step explanation:
The answer is d. None of the above is true.
To calculate velocity, we need to use the equation:
Velocity = M * P / Y
Given:
M = 1,000
P = 2.25
Y = 2,000
Plugging in the values:
Velocity = 1,000 * 2.25 / 2,000
Simplifying:
Velocity = 2.25 / 2
The result is:
Velocity = 1.125
Therefore, the correct answer is: d. None of the above is true.
Learn more about velocity
https://brainly.com/question/30559316
Assume that a professor gives an exam to a class of 50 students. The high score is 98 points and the low score is 48 points. The professor wants to create a frequency distribution that is divided into five classes for the exam scores. The class width for the data is approximately _____________ points.
Answers
Answer:
98-48=50 so the answer is 50