Yesterday, Raina had 129 baseball cards. Today she got c more. Using c, write an expression for the total number of baseball cards she has now.
Answers
Total number of baseball cards will be given by expression 129 + c.
What exactly are expressions?In mathematics, an expression is a combination of numbers, variables, and mathematical operations that represents a value or a quantity. Expressions can be written using various mathematical symbols such as addition, subtraction, multiplication, division, exponents, and parentheses.
Now,
If Raina had 129 baseball cards yesterday and got c more today, then the expression for the total number of baseball cards will be calculated after adding
So,
she has now can be written as:
Total number of baseball cards = 129 + c
Here, c represents the number of additional baseball cards that Raina got today, and the expression 129 + c gives us the total number of baseball cards she has now, including the cards she had yesterday and the new ones she got today.
To know more about expressions visit the link
brainly.com/question/13947055
#SPJ9
Related Questions
A flying squirrel's nest is 60 feet high in a tree. From its nest, the flying squirrel glides 68 feet to reach an acorn that is on the ground. How far is the acorn from the base of the tree?
Answers
Answer:
the acorn is 32 feet from the base of the tree.
Answer:
The acorn is 32 feet from the base of the tree.
Step-by-step explanation:
This is an problem where the Pythagorean Theroem.
The formula is \(a^2+b^2=c^2\) where a & b are the legs and c is the hypotenuse.
In this problem, we are given the height, which is a and the hypotenuse, which the flying squirrel glides, which is c.
We can substitute the values and solve for b which is the distance from the base to the acorn.
The new equation would be \(60^2+b^2=68^2\)
We can simplify the exponents and we get: \(3600+b^2=4624\).
Now, we have to solve for b.
1. Subtract 3600 on both sides: \(b^2=1024\)
2. Take the square root of both sides: \(\sqrt{b^2} =\sqrt{1024}\)
3. Since the exponent and the radical cancel each other, we are left with just b. The square root fo 1024 is 32, which is the value of b.
So the distance from the acorn to the base of the tree is 32 feet.
a) Find the value of k so that the lines and are perpendicular.
b) Determine parametric equations for the plane through the points A(2, 1, 1), B(0, 1, 3), and C(1, 3, −2).
c) Determine a vector equation for the plane that is parallel to the xy -plane and passes through the point (4, 1, 3).
Answers
a) To find the value of k such that the lines and are perpendicular, we need to find the dot product of their direction vectors and set it equal to zero.
The direction vector of the first line is (3, -1, k), and the direction vector of the second line is (2, -2, 5). Taking their dot product, we have:
(3, -1, k) · (2, -2, 5) = 3*2 + (-1)*(-2) + k*5 = 6 + 2 + 5k = 8 + 5k
For the lines to be perpendicular, the dot product must be zero. Therefore, we have:
8 + 5k = 0
Solving this equation, we find:
5k = -8
k = -8/5
So the value of k that makes the lines perpendicular is k = -8/5.
b) To determine parametric equations for the plane through the points A(2, 1, 1), B(0, 1, 3), and C(1, 3, −2), we first need to find two vectors in the plane. We can take the vectors AB and AC. The vector AB is obtained by subtracting the coordinates of point A from those of point B: AB = (0-2, 1-1, 3-1) = (-2, 0, 2). Similarly, the vector AC is obtained by subtracting the coordinates of point A from those of point C: AC = (1-2, 3-1, -2-1) = (-1, 2, -3).
Now, we can express any point (x, y, z) in the plane as a linear combination of these vectors:
(x, y, z) = (2, 1, 1) + s(-2, 0, 2) + t(-1, 2, -3)
where s and t are parameters. These equations represent the parametric equations for the plane through the points A, B, and C.
c) To determine a vector equation for the plane that is parallel to the xy-plane and passes through the point (4, 1, 3), we can use the fact that the normal vector of the xy-plane is (0, 0, 1). Since the plane we are looking for is parallel to the xy-plane, its normal vector will be the same.
Using the point-normal form of a plane equation, the vector equation for the plane is:
(r - r0) · n = 0
where r is a position vector in the plane, r0 is a known point in the plane, and n is the normal vector. Plugging in the values, we have:
(r - (4, 1, 3)) · (0, 0, 1) = 0
Simplifying, we get:
(0, 0, 1) · (x - 4, y - 1, z - 3) = 0
0*(x - 4) + 0*(y - 1) + 1*(z - 3) = 0
z - 3 = 0
Therefore, the vector equation for the plane that is parallel to the xy-plane and passes through the point (4, 1, 3) is z - 3 = 0.
Learn more about perpendicular here:
https://brainly.com/question/11707949
an agronomist measured the heights of n corn plants. the mean height was 220 cm and the standard deviation was 15 cm. calculate the standard error of the mean if (a) n = 25 (b) n = 100
Answers
a. The standard error of the mean for n = 25 is 3 cm
b. The standard error of the mean for n = 100 is 1.5 cm.
Agronomist measured the height of n corn plants. If the mean height is 220 cm and the standard deviation is 15 cm, then we can calculate the standard error of the mean for n = 25 and n = 100 as shown below -
(a) For n = 25:
If n = 25, then the formula for calculating the standard error of the mean is as follows -
Standard Error of the Mean = (Standard Deviation / √n)
Given,
Standard deviation (σ) = 15 cm
Number of samples (n) = 25 cm
We can calculate the standard error of the mean as follows -
Standard Error of the Mean = (Standard Deviation / √n)
= (15 / √25)
= 3
Hence, the standard error of the mean for n = 25 is 3 cm.
(b) For n = 100:
If n = 100, then the formula for calculating the standard error of the mean is as follows -
Standard Error of the Mean = (Standard Deviation / √n)
Given,
Standard deviation (σ) = 15 cm
Number of samples (n) = 100 cm
We can calculate the standard error of the mean as follows -
Standard Error of the Mean = (Standard Deviation / √n)
= (15 / √100)
= 1.5
Hence, the standard error of the mean for n = 100 is 1.5 cm.
Learn more about standard errors:
brainly.com/question/13179711
#SPJ11
Nathan has a points card for a movie theater. He receives 40 rewards points just for signing up. He earns 14.5 points for each visit to the movie theater. He needs at least 225 points for a free movie ticket. What is the least number of visits he needs to make in order to earn a free movie ticket?
Answers
Nathan needs to make 13 visits to make enough points for a movie ticket.
When Nathan joined, he received 40 reward points. This means that out of the 225 points he needs for a movie ticket, he now only needs:
= 225 - 40
= 185 points
He gets 14.5 points for every visit which means that the number of visits he needs to get to 185 points is:
= Number of points remaining / Number of points per visit
= 185 / 14.5
= 12.76 visits
= 13 visits
Nathan therefore needs at least 13 visits to get enough points.
Find out more at https://brainly.com/question/24399290.
Subtract 10x - 7 from 2x – 6.
Answers
(2x - 6) - (10x - 7) # Starting expression
-8x - 1 # Combine like terms
Final answer:
-8x - 1
Hope this helps!
2x-6-10x-7
We group the like and unlike terms
2x-10x-6-7
-8x-14
Simplify the following expression (62)4
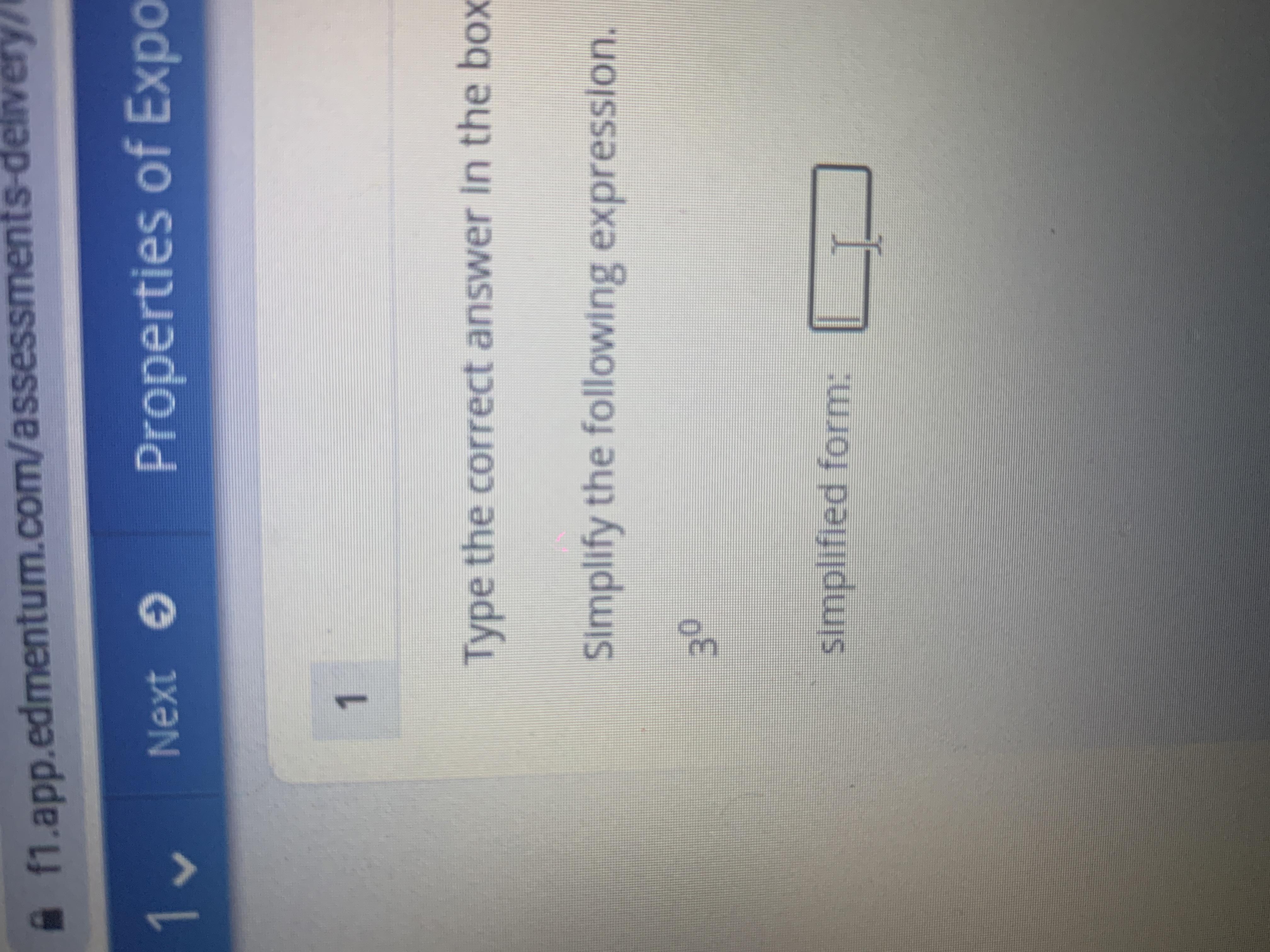
Answers
Answer:
\(3^{0} =1\)
Step-by-step explanation:
SOMEONE HELP ME BEFORE I PASS OUT
1. |X|≤8
2. |X|≤27
Answers
Answer: 1. [-8, 8]
2. [-27, 27]
Step-by-step explanation:
1. |X|≤8
x≤8 or x>=-8
-8<=x<=8 ==> [-8, 8]
2. |X|≤27
x≤27 or x>=-27
-27<=x<=27 ==> [-27, 27]
4. the radius of the larger circle is 10.2 feet. the radius of the smaller circle is 5.4 feet: find the area of the shaded region.
Answers
The area of the shaded region is approximately 18.38 square feet.
To find the area of the shaded region between the larger circle with a radius of 10.2 feet and the smaller circle with a radius of 5.4 feet, we can use the concept of circle sectors.
The area of a circle sector can be calculated by finding the difference between the area of the corresponding triangle and the area of the circular segment.
First, let's calculate the area of the larger circle:
A_large = π(10.2)^2
Next, we calculate the area of the smaller circle:
A_small = π(5.4)^2
To find the area of the shaded region, we need to find the difference between the two circle sectors formed by the radii of the larger and smaller circles.
The angle of the sector formed by the radii can be found using trigonometry. Let's call it θ.
sin(θ) = (10.2 - 5.4) / 10.2
sin(θ) = 0.4706
Using inverse sine, we find θ ≈ 28.15 degrees.
Now we can calculate the area of the shaded region:
Shaded area = (θ / 360°) * A_large - (θ / 360°) * A_small
Shaded area ≈ (28.15 / 360) * π(10.2)^2 - (28.15 / 360) * π(5.4)^2
Shaded area ≈ (0.0782) * π(104.04) - (0.0782) * π(29.16)
Shaded area ≈ 8.1403π - 2.2832π
Shaded area ≈ 5.8571π
Finally, to approximate the value, we use the approximation π ≈ 3.14159:
Shaded area ≈ 5.8571 * 3.14159
Shaded area ≈ 18.38 square feet.
Therefore, the area of the shaded region is approximately 18.38 square feet.
To know more about area refer here:
https://brainly.com/question/3030750#
#SPJ11
- x/7 − 8 = 17
Show work
And check
Answers
Answer:
x = -175
Step-by-step explanation:
Given:
⇒ \(-\frac{x}{7}-8=17\)
Solution:
Work:
\(-\frac{x}{7}-8=17\)
\(-\frac{x}{7}-8+8=17+8\) ⇒ Add 8 to both sides
\(-\frac{x}{7}=25\)
\(7\left(-\frac{x}{7}\right)=25\cdot \:7\) ⇒ Multiply both sides by 7
-x = 175
\(\frac{-x}{-1}=\frac{175}{-1}\) ⇒ Divide both sides by -1
x = -175
Check:
Since, x = -175. We can substitute into the equation to check.
\(-\frac{-175}{7}-8=17\)
\(-\frac{-175}{7}=25\)
\(25-8=17\) ⇒ Statement = True (25 minus 8 is 17.
Hence, x = -175
Lenvy~
Joe started to save money to purchase a new game console. His savings at the end of the first week included a jar of 468 nickels and dimes. The total value of the coins was $34.40. Which system of equations below would be the best to use to find the number of nickels and dimes Anthony had at the end of the first week?
Answers
Answer:
0.05x + 0.10y = 34.40
x + y = 468
Step-by-step explanation:
Step-by-step explanation:
The The guy above is correct
for a data set, half of the observations are always greater than the _______.
Answers
For a data set, half of the observations are always greater than the median. The median is the middle value in a set of data when it is arranged in order of increasing or decreasing magnitude.
It is a measure of central tendency that is more robust to outliers than the mean. The median splits the data set in half, with half of the observations being greater than it and half being less than it.
The median is a crucial measure of central tendency that helps us understand the distribution of a data set. It represents the value that separates the top half of the data from the bottom half. The median is often used as an alternative to the mean when the data set contains outliers or extreme values that can skew the mean. The median is easy to calculate and provides a clear picture of the middle of a data set. Therefore, it is a useful tool for statisticians, researchers, and analysts who need to summarize and describe data sets accurately.
In summary, the median is the value that divides a data set into two equal halves, with half of the observations being greater than it and half being less than it. It is a robust measure of central tendency that is widely used in statistics to describe the distribution of data sets.
To know more about median visit:
brainly.com/question/300591
#SPJ11
a chinese restaurant has a large goldfish pond. suppose that an inlet pipe and a hose together can fill the pond in hours. the inlet pipe alone can complete the job in one hour less time than the hose alone. find the time that the hose can complete the job alone and the time that the inlet pipe can complete the job alone.
Answers
So, the hose can complete the job alone in approximately 2.62 hours, and the inlet pipe can complete the job alone in approximately 1.62 hours.
Let the time it takes for the hose alone to fill the pond be H hours, and the time it takes for the inlet pipe alone be P hours. According to the given information:
1) P = H - 1 (The inlet pipe alone can complete the job in one hour less time than the hose alone)
2) In one hour, the hose fills 1/H of the pond, and the inlet pipe fills 1/P of the pond. Together, they can fill the pond in one hour, so: (1/H) + (1/P) = 1
Now, substitute the value of P from equation 1 into equation 2:
(1/H) + (1/(H-1)) = 1
To solve for H, first find a common denominator (H*(H-1)):
(H-1) + H = H*(H-1)
Combine the terms on the left:
2H - 1 = H^2 - H
Rearrange to form a quadratic equation:
H^2 - 3H + 1 = 0
Now, solve the quadratic equation using the quadratic formula:
\(H = (3 + sqrt(5))/2 or H = (3 - sqrt(5))/2\)
However, since H > 0, the only valid solution is H = (3 + sqrt(5))/2 ≈ 2.62 hours.
Now, find the time it takes for the inlet pipe alone to complete the job:
P = H - 1 = 2.62 - 1 = 1.62 hours
for such more questions on quadratic equation
https://brainly.com/question/1214333
#SPJ11
Helpp (please tell me if you can’t see the numbers so I can tell you them)

Answers
Answer:
-6 is the y coordinate
Step-by-step explanation:
Use the equation below to find the axis of symmetry in the given problem

Answers
-(-20)/2(-2)
20/-4
Axis of Symmetry=5
Camille had $275 in her checking account . she deposited $812 and wrote checks $75, $60, and $48. how much did she have in the account after all these transactions?
Answers
Pleas help me !!! It’s due today

Answers
=0.5x 1.2x10^3x (3.4x10^3)^2=6936000000
A hotel charges a flat rate, x, for each hour a customer
uses the internet.
Enter an equation to express the total cost, y, to use the
internet at the hotel for t hours.
Answers
Answer:
tx=y
Step-by-step explanation:
For every hour you spend on the computer is t. So if it cost x per customer then you can just simply multiply x and t. It says y is the total cost so that would be what is equalls to.
Example:
x= $5
t=3 hours
Using these sample numbers we can put them into the equation
3·5=y
15=y
15 dollars in total
| n | = 3.5 what value for n will make this expression true
This is the I Ready diagnostics.please help me this is due very very soon! Thanks!!
Answers
Answer:
3.5 and -3.5
Step-by-step explanation:
absolute value is the distance from zero to that number so 3.5 and -3.5 should be correct.
Answer:3.5 and -3.5
Step-by-step explanation:
n has absolute value marks, so whatever n is is positive. 3.5 and |-3.5| =3.5
6
How much
10 500
A pile of bricks weighs 22 kg.
18750g of bricks are removed. What weight is left?
Answers
Answer:
3,250g
Step-by-step explanation:
22kg = 22,000g - 18,750g = 3250g
In 2015, around ____ percent of the world’s population had an internet connections.
Answers
Determine the domain of the graph shown
A.0,8
B.0,24
C.0,20
D.0,10
E.0, 12

Answers
A 12-sided solid has faces numbered 1 to 12. The table shows the results of rolling the solid 200
times. Find the experimental probability of rolling a number less than 3
The experimental probability of rolling a number less than 3 is ?
(Simplify your answer.)
Answers
Answer:
there is no picture/screenshot of the table.
Step-by-step explanation:
I could see if I can help but I don't know where the question or the table is.
True or False?
f(x)—> +infinity as x—> 2 for the function f(x)=1/(3x-6)
Answers
Answer:
False
Step-by-step explanation:
Keep in mind both the right and left-side limits of a function have to be equal to each other in order for the limit of the function to exist:
Right side limit: \(\lim_{x \to 2^{+}} \frac{1}{3x-6}=\infty\)
Left-side limit: \(\lim_{x \to 2^{-}} \frac{1}{3x-6}=-\infty\)
Because both side limits do not equal \(\infty\), then the limit does not exist, which means that the statement is false.
You can also see this visually on a graph if you'd wish to plug in the function
PLEASE HELP!!! Triangle ABC is graphed.
(If your answer includes a fraction, enter in fractional form or round to the nearest tenths place.)
1. Find point D that partitions segment AB in a 1.2 ratio.
D=( , )
2. Find point E that partitions segment AC in a 1:2 ratio.
E= ( , )
3. How does triangle ADE relate to triangle ABC?
Triangle ADE is a dilation of triangle ABC by a scale factor of____
using A as the center.

Answers
The coordinates of the point D that partitions the segment in ration 1:2 is D = (4. 3).
What is section formula?The line segment is divided into two pieces by a point, which may or may not be equal. If we know the coordinates of the point, we may calculate the ratio by which the supplied line segment is divided. Also, if we are aware of the ratio that the line segment connecting two places has produced, we may locate the point of division. The two may be accomplished using a section formula from coordinate geometry.
The position of a point that splits a line segment connecting two points into two portions with a length ratio of m:n is found using the section formula.
The coordinates of the point A and B from the given figure is:
A = (1, 3) and B = (10, 3)
The section formula is given as:
(x, y) = (mx2 + nx1 / m+n , my2 + ny1 / m+n)
Substitute the values of m = 1 and n = 2, and the coordinates of the point A and B.
(x, y) = ((1)(10) + (2)(1)/ 3 , (1)(3) + (2)(3) 3)
D(x,y) = (4, 3)
Hence, the coordinates of the point D that partitions the segment in ration 1:2 is D = (4. 3).
Learn more about section formula here:
https://brainly.com/question/30242641
#SPJ1
Mr. Brown's class has 20 students. 6 of the students have blonde hair. What
percent of the students have blonde hair?
Answers
Answer:
30%
Step-by-step explanation:
6/20 = .3
.3 x 100 = 30
6/20=.3
.3x100=30
You invest $20,000 in the stock market. The stock market then plummets
over the next few weeks. Each day, your investment loses half of its value. How
much will you have invested after 14 days? Write the geometric sequence
formula and show all of your work.
Answers
After 14 days, you will have approximately $2.4414 invested in the stock market.
The amount you will have invested after 14 days can be calculated using the geometric sequence formula. The formula for the nth term of a geometric sequence is given by:
an = a1 x \(r^{(n-1)\)
Where:
an is the nth term,
a1 is the first term,
r is the common ratio, and
n is the number of terms.
In this case, the initial investment is $20,000, and each day the investment loses half of its value, which means the common ratio (r) is 1/2. We want to find the value after 14 days, so n = 14.
Substituting the given values into the formula, we have:
a14 = 20000 x\((1/2)^{(14-1)\)
a14 = 20000 x \((1/2)^{13\)
a14 = 20000 x (1/8192)
a14 ≈ 2.4414
Therefore, after 14 days, you will have approximately $2.4414 invested in the stock market.
For more such answers on ratio
https://brainly.com/question/12024093
#SPJ8
The amount you will have invested after 14 days is given as follows:
$2.44.
What is a geometric sequence?A geometric sequence is a sequence of numbers where each term is obtained by multiplying the previous term by a fixed number called the common ratio q.
The explicit formula of the sequence is given as follows:
\(a_n = a_1q^{n-1}\)
In which \(a_1\) is the first term of the sequence.
The parameters for this problem are given as follows:
\(a_1 = 20000, q = 0.5\)
Hence the amount after 14 days is given as follows:
\(a_{14} = 20000(0.5)^{13}\)
\(a_{14} = 2.44\)
More can be learned about geometric sequences at https://brainly.com/question/24643676
#SPJ1
Is anyone able to help me on this?? I need serious help! Thank ya!

Answers
Answer:
The function is f(x)=2x
Step-by-step explanation:
Since every single y is 2 times x, it will be 2x. This function just doubles whatever x you put in.
Answer:
Step-by-step explanation:
Those are coordinate points on a line but they are written in table form.
For the first point, when x=1, y=2 (that's given from the table) but it's a point on the line (1, 2)
The next point (2,4),
(3,6) and so forth.
The format for a line is
y=mx+b (slope-intercept form)
or
\(y-y_{1} = m(x-x_{2})\) (point-slope form)
They did not give you the y-intercept (that's when x=0) in the chart. You may have been able to figure it out by looking at the pattern but if not we will use the second formula, point slope form, because we know a point from the chart and we can find slope
\(slope=m=\frac{y_{2}- y_{1} }{x_{2}- x_{1} }\)
pick any 2 points from the chart to find slope. I will pick (1,2) and (2,4)
\(m=\frac{4-2}{2-1 } =\frac{2}{1} =2\)
Now that i know slope m=2 and i will pick (1,2) to plug into formula
\(y-y_{1} = m(x-x_{2})\)
y-2=2(x-1) distribute 2
y-2=2x-2 add 2 to both sides
y=2x
The function is increasing at a rate of 2 and the y-intercept is 0.
how to find the perimeter of a rhombus using diagonals
Answers
A rhombus is a quadrilateral that has four sides of equal length. A rhombus also has two diagonals, which are perpendicular bisectors of each other. This formula is given as follows: Perimeter = 4 × a, where a is the length of each side of the rhombus.
To find the perimeter of a rhombus using diagonals, follow these steps:
Step 1: Obtain the length of each diagonal of the rhombus.
Step 2: Use the length of the diagonals to find the length of each side.
Step 3: Add the length of each side to find the perimeter of the rhombus.
The perimeter is the sum of all the sides of a figure. To get the perimeter of a rhombus using diagonals, the length of each diagonal has to be found first. The formula for finding the length of each side of a rhombus is: where the diagonal is the measure of the diagonal of the rhombus.
To find the perimeter of a rhombus, add the length of all the sides of the rhombus. This formula is given as follows: Perimeter = 4 × a, where a is the length of each side of the rhombus.
Therefore, the perimeter of a rhombus using diagonals can be found by following the above procedure and then using the formula to add all the sides of the rhombus.
Learn more about Perimeter from the given link
https://brainly.com/question/7486523
#SPJ11
Sixth grade is going on a field trip to Disney World. Tickets will cost each student $75.36. Parent tickets will cost $82.79 each. What will the total cost be for 36 students and 45 parents
Answers
Answer:
$ 6,438.51
Step-by-step explanation:
75.36 X 36 = 2,712.96
82.79 X 45 = 3,725.55
2,712.96 + 3,725.55 = 6,438.51
do 1/9 and 6/54 form a proportion? and WHY? show steps:
Answers
Answer:
Step-by-step explanation:
Two ratios are proportional if their cross products are equal. That is, if we multiply the numerator of one ratio by the denominator of the other ratio, the result should be equal to the product of the denominator of the first ratio with the numerator of the second ratio.
Let's see if this holds true for 1/9 and 6/54:
(1 x 54) = 54
(9 x 6) = 54
Since the cross products are equal, we can say that 1/9 and 6/54 are proportional.
To simplify the ratio, we can divide the numerator and denominator by their greatest common factor (GCF), which is 3.
1/9 ÷ 3/3 = 1/27
6/54 ÷ 3/3 = 2/18 = 1/9
Thus, the simplified ratio of 1/9 and 6/54 is 1/9, and we can see that 1/9 and 6/54 are in fact proportional.